
【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
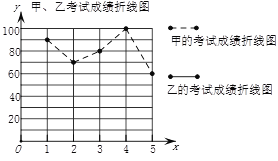
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)
【答案】(1)80,80;(2)见解析;(3)S2乙=80;(4)乙.
【解析】
(1)根据总成绩相同和平均数的计算公式计算即可;
(2)根据乙的成绩在图中描点连线即可;
(3)根据方差的计算公式计算即可;
(4)根据平均数和方差的性质进行判断即可.
解:(1)∵甲、乙总成绩相同,
∴90+70+80+100+60=70+90+90+a+70,
解得a=80,
![]() =
=![]() =80,
=80,
故答案为80,80;
(2)如图所示:
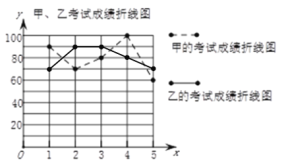
(3)S2乙=![]() ×[(70-80)2+(90-80)2+(90-80)2+(80-80)2+(70-80)2]=80;
×[(70-80)2+(90-80)2+(90-80)2+(80-80)2+(70-80)2]=80;
(4)∵甲、乙总成绩相同,
∴![]() =
=![]() ,
,
∵S2甲=200,S2乙=80,
∴S2甲> S2乙,
∴乙的成绩比甲的成绩稳定,
∴从平均数和方差的角度分析,乙将被选中.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
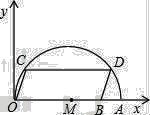
【题目】如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() .与
.与![]() 轴负半轴交于点
轴负半轴交于点![]() ,在下面五个结论中:
,在下面五个结论中:
①![]() ;②
;②![]() ;③
;③![]() ;④只有当
;④只有当![]() 时,
时,![]() 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使![]() 为等腰三角形的
为等腰三角形的![]() 值可以有四个.
值可以有四个.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=35°,以C为旅转中心,将△ABC旋转到△A′B′C的位置,点B在边A′B′上,则∠BDC为( )
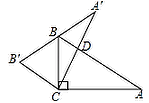
A.70°B.90°C.100°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标都是整数的点叫作整点,直线y=kx-3(k>0),与坐标轴围成的三角形内部(不包含边界)有且只有三个整点,则k的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能环保的油电混合动力汽车,既可用油做动力行驶,也可用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求汽车行驶中每千米用电费用是多少元?
(2)甲、乙两地的距离是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
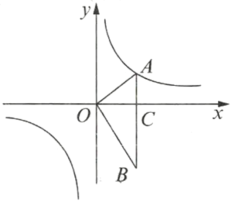
【题目】如图,在平面直角坐标系中,![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上.
的图像上.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求![]() 面积;
面积;
(3)在坐标轴上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点
三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,简述你的理由.
的坐标;若不存在,简述你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com