
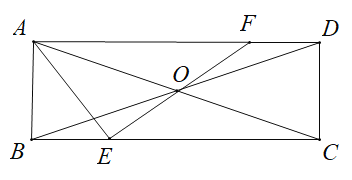
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 和
和![]() 交于点
交于点![]() ,点
,点![]() 是边
是边![]() 上的动点(不与点
上的动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长为_____.
的长为_____.
【答案】![]() ,1,
,1,![]() 或
或![]()
【解析】
先由矩形的性质可得AD=BC=3,![]() ,
,![]() ,然后根据全等三角形的判定方法证得
,然后根据全等三角形的判定方法证得![]() ,进而可得
,进而可得![]() ,设
,设![]() ,则
,则![]() .当
.当![]() 是等腰三角形时,分
是等腰三角形时,分![]() ,
,![]() ,
,![]() 三种情况,分别列出关于a的方程,解方程即可.
三种情况,分别列出关于a的方程,解方程即可.
∵四边形![]() 是矩形,
是矩形,
∴AD=BC=3,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
设![]() ,则
,则![]() .
.
当![]() 是等腰三角形时,分三种情况讨论.
是等腰三角形时,分三种情况讨论.
①如图(1),当![]() 时,
时,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
解得![]() .
.
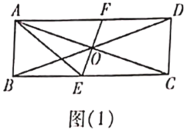
②如图(2),当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,
,
则四边形ABEH是矩形,AH=FH
∴AH=BE
即![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.
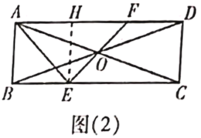
③如图(3),当![]() 时,
时,![]() .
.
又![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,
∴EF=AF=3-a,FG=EF-EG=3-a-a=3-2a,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
解得![]() ,
,![]() .
.
综上所述,![]() 的长为
的长为![]() ,1,
,1,![]() 或
或![]()
故答案为:![]() ,1,
,1,![]() 或
或![]()


科目:初中数学 来源: 题型:
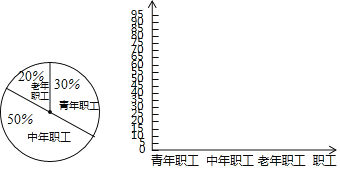
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知正比例函数
中,已知正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
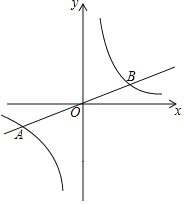
(1)反比例函数的解析式为____________,点![]() 的坐标为___________;
的坐标为___________;
(2)观察图像,直接写出![]() 的解集;
的解集;
(3)![]() 是第一象限内反比例函数的图象上一点,过点
是第一象限内反比例函数的图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为3,求点
的面积为3,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“村村通公路政策,是近年来国家构建和谐社会,支持新农村建设的一项重大公共决策,是一项民心工程,惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目,经调查:甲、乙两队单独完成该工程,乙队所需时间是甲队的2倍;甲、乙两队共同完成该工程需30天;若甲队每天所需劳务费用为2400元,乙队每天所需劳务费用为1500元,从节约资金的角度考虑,应选择哪个工程队更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.
(1)如图(1),![]() 是中垂三角形,
是中垂三角形,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的中线,且
边上的中线,且![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
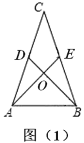


(2)如图(2),在中垂三角形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中线,且
上的中线,且![]() 于点
于点![]() ,猜想
,猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
(3)如图(3),四边形![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 并延长,交于点
并延长,交于点![]() .
.
①求证:![]() 是中垂三角形;
是中垂三角形;
②若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
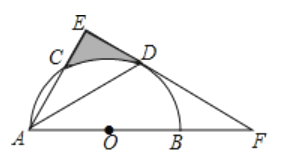
(1)求证:EF为半圆O的切线.
(2)若AO=BF=2,求阴影区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,CD是中线,
,CD是中线,![]() ,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
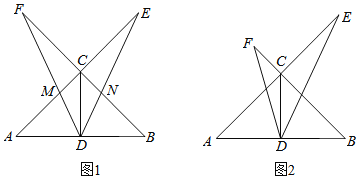
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,在![]() 绕点D旋转的过程中,试证明
绕点D旋转的过程中,试证明![]() 恒成立;
恒成立;
(3)若![]() ,
,![]() ,求DN的长.
,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
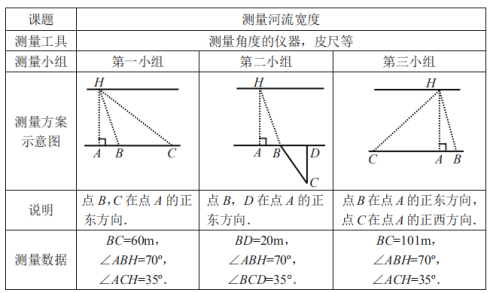
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到0.1m).
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com