
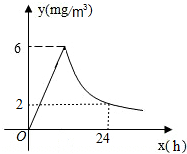
 每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中的含药量y(mg/m3)与时间x(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m3且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m3时,持续时间可以达到12h.
每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中的含药量y(mg/m3)与时间x(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m3且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m3时,持续时间可以达到12h. 分析 首先根据已知点的坐标确定反比例函数的解析式,然后确定两个函数的交点的横坐标,从而确定正比例函数的解析式,最后令两个函数值等于3求得时间相减即可.
解答 解:∵反比例函数经过点(24,2),
∴反比例函数的解析式为y=$\frac{48}{x}$,
令y=6,解得:x=8,
∴直线与双曲线的交点坐标为(8,6),
∴正比例函数的解析式为y=$\frac{3}{4}$x,
令y=$\frac{48}{x}$=3,解得:x=16,
令y=$\frac{3}{4}$x=3,解得:x=4,
∴当空气中的含药量不低于3mg/m3时,持续时间可以达到16-4=12h,
故答案为:12.
点评 本题考查了反比例函数及正比例函数的应用,解题的关键是能够从实际问题中抽象出反比例函数和正比例函数模型,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )| A. | 3.5 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
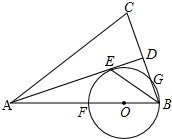 已知:如图,△ABC中,AB=AC,AD平分∠BAC,BE平分∠ABC交AD于点E.经过B、E两点的⊙O交AB于点F,交BC于点G,BF恰为⊙O的直径.
已知:如图,△ABC中,AB=AC,AD平分∠BAC,BE平分∠ABC交AD于点E.经过B、E两点的⊙O交AB于点F,交BC于点G,BF恰为⊙O的直径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com