[题目]如图.在△ABC中.∠B=45°.∠C=60°.AC=20．(1)求BC的长度,(2)若∠ADC=75°.求CD的长．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC中，∠B=45°，∠C=60°，AC=20．

（1）求BC的长度；

（2）若∠ADC=75°，求CD的长．

【答案】（1）10+10；（2）20﹣20

【解析】分析：(1)、分别根据Rt△ACE和Rt△ABE的性质求出CE和BE的长度，从而得出BC的长度；(2)、根据内角和定理求出∠BAC的度数，然后结合公共角得出△CDA和△CAB相似，从而得出CD的长度．

详解：（1）作AE⊥BC于E，如图，在Rt△ACE中，∵∠C=60°，

∴CE=AC=10，AE=CE=10，

在Rt△ABE中，∵∠B=45°，∴BE=AE=10，∴BC=BE+CE=10+10；

（2）∵∠BAC=180°﹣45°﹣60°=75°，而∠ADC=75°，∴∠ADC=∠ABC，∵∠ACD=∠BCA，

∴△CDA∽△CAB，∴=，即=，∴CD=20﹣20．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

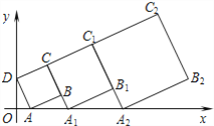
【题目】在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1,………按这样的规律进行下去，正方形A2018B2018C2018C2017的面积为（）

A. B. C. D.

查看答案和解析>>

科目：初中数学 来源： 题型：

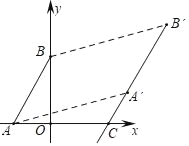
【题目】如图，已知A（﹣2，0），B（0，4），将线段AB平移到第一象限得线段A′B′，点A′的横坐标为5，若作直线A′B′交x轴于点C（4，0）．

（1）求线段AB所在直线的解析式；

（2）直线AB上一点P（m，n），求出m、n之间的数量关系；

（3）若点Q在y轴上，求QA′+QB′的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

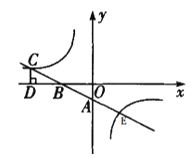
【题目】如图，一次函数y＝x－1的图象与坐标轴分别交于A、B两点，与反比例函数y＝的图象在第二象限的交点为点C，CD⊥x轴，垂足为点D，若C点横坐标为－4，

(1)反比例函数的关系式及E点坐标；

(2)利用图像，当x<0时，写出的解集．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在正方形ABCD对角线BD上截取BE=BC，连接CE并延长交AD于点F，连接AE，过B作BG⊥AE于点G，交AD于点H，则下列结论错误的是（　　）

A. AH=DF B. S四边形EFHG=S△DCF+S△AGH

C. ∠AEF=45° D. △ABH≌△DCF

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在一个不透明的袋中装有5个只有颜色不同的球，其中3个黄球，2个黑球．

（1）求从袋中同时摸出的两个球都是黄球的概率；

（2）现将黑球和白球若干个（黑球个数是白球个数的2倍）放入袋中，搅匀后，若从袋中摸出一个球是黑球的概率是，求放入袋中的黑球的个数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某书店积极响应政府“改革创新，奋发有为”的号召，举办“读书节“系列活动．活动中故事类图书的标价是典籍类图书标价的1.5倍，若顾客用540元购买图书，能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本．

（1）求活动中典籍类图书的标价；

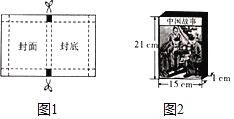
（2）该店经理为鼓励广大读者购书，免费为购买故事类的读者赠送图1所示的精致矩形包书纸．在图1的包书纸示意图中，虚线是折痕，阴影是裁剪掉的部分，四角均为大小相同的正方形，正方形的边长为折叠进去的宽度．已知该包书纸的面积为875cm2（含阴影部分），且正好可以包好图2中的《中国故事》这本书，该书的长为21cm，宽为15cm，厚为1cm，请直接写出该包书纸包这本书时折叠进去的宽度．