
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
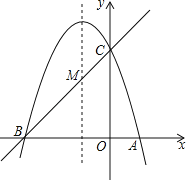
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标:
(3)在抛物线上存在点P(不与C重合),使得△APB的面积与△ACB的面积相等,求点P的坐标.
【答案】(1)y=﹣x2﹣2x+3,y=x+3;(2)点M(﹣1,2);(3)点P的坐标为:(﹣2,3)或(![]() ,﹣3)或(
,﹣3)或(![]() ,﹣3).
,﹣3).
【解析】
(1)根据抛物线的对称性求出B(﹣3,0),然后可设交点式为y=a(x﹣1)(x+3),代入(0,3)求出a即可;然后再根据B、C坐标利用待定系数法求直线BC的解析式即可;
(2)点A关于抛物线对称轴的对称点为点B,直线BC交抛物线对称轴于点M,则点M即为所求,据此即可得解;
(3)△APB的面积与△ACB的面积相等,则|yP|=yC=3,即x22x+3=±3,求解即可.
(1)∵抛物线经过A(1,0),且对称轴为直线x=﹣1,
∴点B(﹣3,0),
设抛物线的表达式为:y=a(x﹣1)(x+3),
代入C(0,3)得:3=a×(﹣1)×3,
解得:a=﹣1,
故抛物线的表达式为:y=﹣(x﹣1)(x+3)=﹣x2﹣2x+3;
由直线BC的解析式为:y=mx+n,
代入B(﹣3,0),C(0,3)得:![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为:y=x+3;
(2)点A关于抛物线对称轴的对称点为点B(﹣3,0),直线BC交函数对称轴于点M,则点M即为所求,
∵直线BC的解析式为:y=x+3,
当x=﹣1时,y=2,
∴点M(﹣1,2);
(3)△APB的面积与△ACB的面积相等,则|yP|=yC=3,
即﹣x2﹣2x+3=±3,
当﹣x2﹣2x+3=3时,解得:x1=-2,x2=0(舍去),
当﹣x2﹣2x+3=-3时,解得:x1=![]() ,x2=
,x2=![]() ,
,
故点P的坐标为:(﹣2,3)或(![]() ,﹣3)或(
,﹣3)或(![]() ,﹣3).
,﹣3).


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】学生会8位干部每次轮流3位干部对同学的日常规范进行检查.每两次检查后,由轮流到的第1位干部公布检查情况.8位干部依次记为a1,a2,a3,…,a8,具体为:第1次由a1,a2,a3三位干部轮值,且不需公布检查情况;第2次由a4,a5,a6三位干部轮值,且由a4公布检查情况;第3次由a7,a8,a1三位干部轮值,且不需公布检查情况;依此下去…,则第124次轮值的干部与公布情况应该为( )
A.![]() ,
,![]() ,
,![]() ,且由
,且由![]() 公布B.
公布B.![]() ,
,![]() ,
,![]() ,且由
,且由![]() 公布
公布
C.![]() ,
,![]() ,
,![]() ,且不需公布D.
,且不需公布D. ![]() ,
,![]() ,
,![]() ,且不需公布
,且不需公布
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
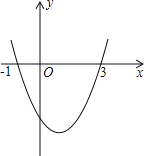
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(-1,y1),(2,y2),(3,y3)在反比例函数![]() 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y2>y3>y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com