
【题目】如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.

(1)求证:F为BC中点.
(2)若OB⊥AC,OF=1,求平行四边形ABCD的周长.
【答案】(1)见解析;(2)平行四边形ABCD的周长为8.
【解析】
(1)先证明OB=OD,再证得EC//OD,EC=OD,进而得到OB//EC,OB=EC,说明四边形OBEC为平行四边形,最后根据平行四边形的性质即可证明;
(2)先证明四边形ABCD平行四边形,再证明平行四边形DOEC是矩形,求得BC,即可求得菱形ABCD的周长.
(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵四边形DOEC为平行四边形,
∴OD∥EC,OD=EC,
∴EC∥OB,EC=OB,
∴四边形OBEC为平行四边形,
∴BF=CF,即F为BC中点;
(2)解:∵四边形ABCD是平行四边形,OB⊥AC,
∴四边形ABCD是菱形,
∵四边形OBEC为平行四边形,OB⊥AC,
∴四边形OBEC为矩形,
∴BC=OE=2OF,
∵OF=1,
∴BC=2,
∴平行四边形ABCD的周长=4BC=8.


科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图像上,已知点B的坐标是(![]() ,
,![]() ),则k的值为( )
),则k的值为( )
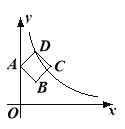
A.10 B.8 C.6 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“京张高铁”是2022年北京冬奥会的重要交通基础设施,考虑到不同路段的特殊情况,将根据不同的运行区间设置不同的时速.其中北京北站到清河站分为地下的清华园隧道12千米和地上的清河段10千米两部分,地下与地上的运行速度之比为![]() ,地下比地上的运行时间多2分钟,求通过地下的清华园隧道所需的速度.
,地下比地上的运行时间多2分钟,求通过地下的清华园隧道所需的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
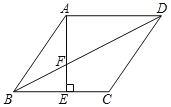
【题目】菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
①BF为∠ABE的角平分线;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正确的为( )
.其中正确的为( )
A.①③B.①②④C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③三次函数
;③三次函数![]() 的图象与x轴交点的横坐标分别为a和b,则
的图象与x轴交点的横坐标分别为a和b,则![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
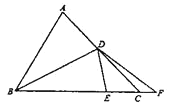
【题目】在![]() ABC中,∠ACB=45°, D为AC上一点,
ABC中,∠ACB=45°, D为AC上一点,![]() ,连接BD,将
,连接BD,将![]() ABD沿BD翻折至
ABD沿BD翻折至![]() EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,
EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,![]() ,则DF长为( )
,则DF长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
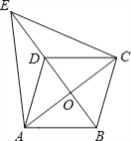
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com