
【题目】实验证明,平面镜反射光线的规律是:照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
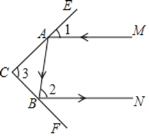
如图,一束光线MA照射到平面镜CE上,被CE反射到平面镜CF上,又被CF反射.已知被CF反射出的光线BN与光线MA平行.若∠1=35°,则∠2= ,∠3= ;若∠1=50°,∠3= .
(2)由(1)猜想:当两平面镜CE,CF的夹角∠3为多少度时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行,请你写出推理过程.
【答案】(1)70°,90°,90°;(2)猜想:当两平面镜CE,CF的夹角∠3为90°时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行.理由见解析.
【解析】
(1)根据平行线的性质和三角形内角和,以及入射角等于反射角,可以求得∠2和∠3的度数;
(2)先写出∠3等于多少度,然后根据题意和图形结合第(1)问的提示思路,即可写出推理过程.
解:(1)∵AM∥BN,
∴∠MAB+∠2=180°,
∵∠MAB+∠1+∠BAC=180°,∠1=∠BAC,∠1=35°,
∴∠2=2∠1=70°,
∵∠2+∠ABC+∠NBF=180°,∠ABC=∠NBF,
∴∠ABC=55°,
∴∠3=180°-∠BAC-∠ABC=90°;
当∠1=50°时, 同理可得,∠2=100°,∠ABC=40°,∠BAC=∠1=50°,
则∠3=180°-∠BAC-∠ABC=90°;
故答案为:70°,90°,90°;
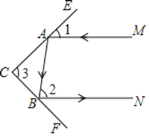
(2)猜想:当两平面镜CE,CF的夹角∠3为90°时,可以使任何射到平面镜CE上的光线MA,经过平面镜CE,CF的两次反射后,入射光线MA与反射光线BN平行.
理由:∵∠3=90°,
∴∠BAC+∠ABC=90°,
∵∠1=∠BAC,∠ABC=∠NBF,
∴∠BAC+∠1+∠ABC+∠NBF=180°,
∴∠MAB+∠2=180°,
∴MA∥BN.


科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲有存款600元,乙有存款2000元,从本月开始,他们进行零存整取储蓄,甲每月存款500元,乙每月存款200元.
(1)列出甲、乙的存款额y1、y2(元)与存款月数x(月)之间的函数关系式,画出函数图象.
(2)请问到第几个月,甲的存款额超过乙的存款额?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的 ![]() 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.
(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x满足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知分式A=![]() .
.
(1) 化简这个分式;
(2) 当a>2时,把分式A化简结果的分子与分母同时加上3后得到分式B,问:分式B的值较原来分式A的值是变大了还是变小了?试说明理由.
(3) 若A的值是整数,且a也为整数,求出符合条件的所有a值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,一次函数y=kx+b的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点.
两点.
(1)求一次函数和反比例函数的解析式;
(2)设点![]() 和
和![]() 是反比例函数
是反比例函数![]() 图象上两点,若
图象上两点,若![]() ,求
,求![]() 的值;
的值;
(3)若M(x1,y1)和N(x2,y2)两点在直线AB上,如图2所示,过M、N两点分别作y轴的平行线交双曲线于E、F,已知﹣3<x1<0,x2>1,请探究当x1、x2满足什么关系时,MN∥EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
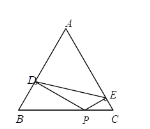
【题目】如图,△ABC 是等边三角形,P 是 BC 上任意一点,PD⊥AB,PE⊥AC,连接 DE.记△ADE 的周长为![]() ,四边形 BDEC 的周长为
,四边形 BDEC 的周长为![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A. ![]() =
=![]() B.
B. ![]() >
>![]() C.
C. ![]() <
<![]() D. 无法确定
D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某移动通信公司推出了如下两种移动电话计费方式,
月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) | |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)
(1)请根据题意完成如表的填空;
月主叫时间500分钟 | 月主叫时间800分钟 | |
方式一收费/元 |
| 130 |
方式二收费/元 | 50 |
|
(2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com