
分析 (1)根据减法的性质去掉括号,再计算即可;
(2)根据有理数的加减混合计算顺序计算,注意应用交换律和结合律.
解答 解:(1)(-2$\frac{1}{5}$)+(+3.2)-(-4.6)+(-3.2)
=3.2-3.2+4.6-2.2
=2.4;
(2)$\frac{3}{5}$+(-$\frac{3}{4}$)+(-2$\frac{3}{5}$)+(-$\frac{1}{4}$)+1$\frac{1}{17}$
=$\frac{3}{5}-2\frac{3}{5}-\frac{3}{4}-\frac{1}{4}+1\frac{1}{17}$
=-2-1+$1\frac{1}{17}$
=-$1\frac{16}{17}$.
点评 本题考查了有理数加减混合计算,注意减法的性质:减去两个数的差等于减去被减数,加上减数.


科目:初中数学 来源: 题型:解答题
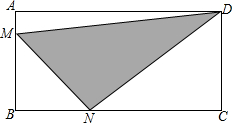 如图,矩形ABCD中,AB=6cm,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动.若M,N分别从A,B点同时出发,设移动时间为t(0<t<6),△DMN的面积为S.
如图,矩形ABCD中,AB=6cm,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动.若M,N分别从A,B点同时出发,设移动时间为t(0<t<6),△DMN的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
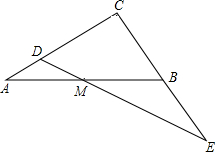 如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.
如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
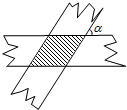 如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.
如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com