Question

12．在△ABC中，D，E分别在AB，AC的反向延长线上，DE∥BC，若AD：AB=3：4，EC=14厘米，则AC=8厘米．

Answer 1

分析 先根据题意画出图形，再根据DE∥BC得出$\frac{AC}{EC}$=$\frac{4}{7}$，最后把EC=14代入计算即可．

解答 解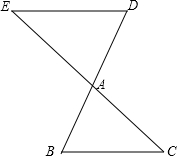：根据题意画图如下：
∵DE∥BC，
∴△ABC∽△ADE，
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{3}{4}$，
∴$\frac{AC}{EC}$=$\frac{4}{7}$，
∵EC=14厘米，
∴$\frac{AC}{14}$=$\frac{4}{7}$，
∴AC=8（厘米）．
故答案为：8厘米．

点评 本题考查平行线分线段成比例定理，找准对应关系，得出$\frac{AE}{AC}$=$\frac{AD}{AB}$是解决本题的关键．