
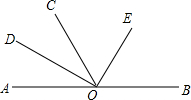
 如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.
如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数. 分析 根据平角可得:∠A0D+∠COD+∠COE+∠EOB=180°,由∠A0D=∠COD,∠COE=∠EOB,求出∠DOE=90°,由∠DOC:∠COE=2:3,即可求出∠COD与∠COE的度数.
解答 解:由图可知:∠A0D+∠COD+∠COE+∠EOB=180°,
∵∠A0D=∠COD,∠COE=∠EOB,
∴2∠COD+2∠COE=180°,
∴∠COD+∠COE=90°,
∴∠DOE=90°,
∵∠DOC:∠COE=2:3,
∴∠DOC=$\frac{2}{5}$∠DOE=$\frac{2}{5}×9{0}^{°}$=36°,∠COE=$\frac{3}{5}×∠DOE$=$\frac{3}{5}×90°$=54°,.
点评 本题考查了角的计算,解决本题的关键是掌握角平分线的性质.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 试验次数 | 20 | 40 | 60 | 80 | 100 |
| “和为2”的频数 | 6 | 8 | 14 | 24 | 27 |
| “和为2”的频率 | 0.30 | 0.20 | 0.23 | 0.30 | 0.27 |
| 试验次数 | 120 | 140 | 160 | 180 | 200 |
| “和为2”的频数 | 28 | 38 | 42 | 46 | 49 |
| “和为2”的频率 | 0.23 | 0.27 | 0.26 | 0.27 | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com