Question

（本题满分12分）如图，在平面直角系中，点A、B分别在x轴、y轴上，A（8，0），B（0，6），点P从点B出发，沿BA以每秒1个单位的速度向点A运动，点Q从点A出发，沿AO以每秒1个单位的速度向点O运动，当点Q到达点O时，两点同时停止运动，设点Q的运动时间为t秒．

（1）用含t的代数式表示C点坐标；

（2）如图1，连接PQ，过点Q作QC⊥AO交AB于点C，在整个运动过程中，当t为何值时，△CPQ为等腰三角形？

（3）如图2，以QC为直径作⊙D，⊙D与AB的另一个公共点为E．问是否存在某一时刻t，使得以BC、CE、AE的长为边的三角形为直角三角形？若存在，直接写出一个符合题意的t的值；若不存在，请说明理由．

 

Answer 1

（1）C（，）；（2）或或或；（3）或．

【解析】

试题分析：（1）根据勾股定理可求出AB=10，易证△AQC∽△AOB，由此可用t的代数式表示出QC、OQ的长，从而解决问题．

（2）可分四种情况（图a、图b、图c、图d），只需用t的代数式表示出相关线段的长，然后建立方程，就可求出对应t的值．

（3）先用t的代数式表示出BC、CE、AE的长，可证AE＞CE，只需分两种情况（BC为斜边、AE为斜边）进行讨论，运用勾股定理建立方程，就可求出符合题意的t的值．

试题解析：（1）∵A（8，0），B（0，6），∴OA=8，OB=6．

∵∠AOB=90°，∴AB=10．

∵QC⊥AO，∴∠CQA=90°=∠BOA，∴QC∥OB，∴△AQC∽△AOB．

∴．

∵OA=8，OB=6，AB=10，AQ=t，∴，∴QC=，AC=．

∵OQ=OA﹣AQ=，∴点C的坐标为（，）．

（2）①如图a，CP=CQ．

∵CP=AB﹣BP﹣AC=，CQ=，∴，解得：．

②如图b，PC=PQ．

∵∠CQA=90°，∴∠PCQ+∠QAC=90°，∠PQC+∠AQP=90°．

∵PC=PQ，∴∠PCQ=∠PQC，∴∠AQP=∠QAC，∴PQ=PA，∴PC=PA，∴AC=2AP．

∵AC=，AP=，∴．解得：．

③如图c，CQ=CP．

∵CQ=，CP=，∴，解得：．

④如图d，QC=QP．

过点Q作QN⊥AC于点N，

则有PN=CN=PC=．

∵QC∥OB，∴∠QCN=∠OBA．

∵∠CNQ=∠BOA=90°，∴△CNQ∽△BOA，∴，∴CN•AB=OB•CQ，∴，

解得：．

综上所述：当t取或或或时，△CPQ是等腰三角形．

（3）如图e，连接QE．

∵CQ是⊙D的直径，∴∠CEQ=90°．∴∠QEA=90°=∠BOA．

∵∠EAQ=∠OAB，∴△QEA∽△BOA，∴．∴AE=．

∴CE=AC﹣AE=，BC=．

∵，∴AE＞CE．∴CE不可能是斜边．

①BC为斜边，

则有．∴，整理得：，

解得：，，∵，∴．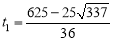

②AE为斜边，

则有．∴．整理得：．

解得：，，∵，∴．

综上所述：符合题意的t的值为或．

考点：1．圆的综合题；2．解一元二次方程-公式法；3．等腰三角形的判定与性质；4．相似三角形的判定与性质．