
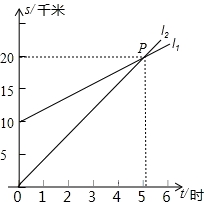
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
(1)当时间为0时,甲离A地__________千米;
(2)当时间为__________时,甲、乙两人离A地距离相等;
(3)图中P点的坐标是__________;
(4)l1对应的函数表达式是:S1=__________;
(5)当t=2时,甲离A地的距离是__________千米;
(6)当S=28时,乙离开A地的时间是__________时.
【考点】一次函数的应用.
【专题】推理填空题.
【分析】(1)由图象可以得到当时间为0时,甲离A地的距离是多少;
(2)由图象可以得到甲、乙两人离A地距离相等时的时间;
(3)由图象可以得到点P的坐标;
(4)设出l1对应的函数表达式,然后根据点(0,10),(5,20)在此函数的图象上,可以求得相应的函数解析式;
(5)将t=2代入l1的函数解析式,可以求得S1的值,从而可以解答本题;
(6)设出l2对应的函数表达式,然后根据点(5,20)在此函数的图象上,可以求得l2对应的函数表达式,然后令S2=28,可以求得相应的t的值,本题得以解决.
【解答】解:(1)由图象可知,当时间为0时,甲离A地10千米,
故答案为:10;
(2)由图象可知,当时间等于5时,甲、乙两人离A地距离相等;
故答案为:5;
(3)由图象可得,点P的坐标为(5,20);
故答案为:(5,20);
(4)设l1对应的函数表达式是:S1=kt+b,
∵点(0,10),(5,20)在此函数的图象上,
∴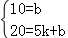
解得,k=2,b=10
即l1对应的函数表达式是:S1=2t+10,
故答案为:2t+10;
(5)当t=2时,S1=2×2+10=14千米,
故答案为:14;
(6)设l2对应的函数表达式是:S2=mt,
∵点(5,20)在此函数的图象上,
∴20=5m,
解得,m=4,
即l2对应的函数表达式是:S2=4t,
令S2=28时,28=4t,得t=7,
故答案为:7.
【点评】本题考查一次函数的应用,解题的关键是明确题意,利用数形结合的思想解答问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,直线y=k1x+b与反比例函数y=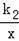
 (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求k1和k2的值;
(2)结合图象直接写出k1x+b﹣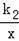
 >0的x的取值范围.
>0的x的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
2016年“龙岗年货博览会”在大运中心体育馆展销,小丽从家出发前去购物,途中发现忘了带钱,于是打电话让妈妈马上从家里送来,同时小丽也往回走,遇到妈妈后聊了一会儿,接着继续前往大运中心体育馆.设小丽从家出发后所用时间为t,小丽与体育馆的距离为S,下面能反映S与t的函数关系的大致图象是( )
A.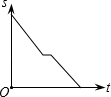 B.
B.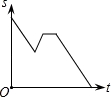 C.
C.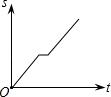 D.
D.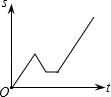
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com