
如图,直线y=k1x+b与反比例函数y=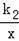
 (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求k1和k2的值;
(2)结合图象直接写出k1x+b﹣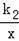
 >0的x的取值范围.
>0的x的取值范围.


【考点】反比例函数与一次函数的交点问题.
【分析】(1)先把A(1,6)代入y=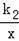
 得到k2=1×6=6,再把B(3,a)代入y=
得到k2=1×6=6,再把B(3,a)代入y=
 得a=2,则B点坐标为(2,3),然后利用待定系数法求一次函数的解析式,得到k1的值;
得a=2,则B点坐标为(2,3),然后利用待定系数法求一次函数的解析式,得到k1的值;
(2)根据函数的图象结合A、B的坐标即可求得.
【解答】解:(1)∵直线y=k1x+b与反比例函数y=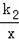
 (x>0)的图象交于A(1,6),B(a,3)两点,
(x>0)的图象交于A(1,6),B(a,3)两点,
∴k2=1×6=6,3a=6,即a=2,
∴B点坐标为(2,3),
∵一次函数y=k1x+b的图象过A(1,6),B(2,3)两点,
∴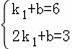
 ,
,
解得
 ,
,
∴k1=﹣3,k2=6;
(2)k1x+b﹣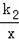
 >0的x的取值范围为1<x<2.
>0的x的取值范围为1<x<2.
【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标同时满足两个函数的解析式;求反比例函数图象与一次函数图象的交点坐标就是把两个图象的解析式组成方程组,方程组的解就是交点的坐标.也考查了待定系数法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
(1)图中第六行括号里的数字分别是__________;(请按从左到右的顺序填写)
(2)(a+b)4=__________;
(3)利用上面的规律计算求值:(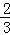 )4﹣4×(
)4﹣4×(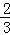 )3+6×(
)3+6×(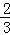 )2﹣4×
)2﹣4×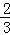 +1.
+1.
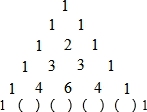
查看答案和解析>>
科目:初中数学 来源: 题型:
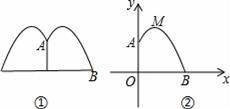
如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),如果不考虑其他因素,那么水池的半径至少要 m,才能使喷出的水流不至落到池外.

查看答案和解析>>
科目:初中数学 来源: 题型:
张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2.
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
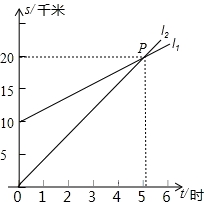
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
(1)当时间为0时,甲离A地__________千米;
(2)当时间为__________时,甲、乙两人离A地距离相等;
(3)图中P点的坐标是__________;
(4)l1对应的函数表达式是:S1=__________;
(5)当t=2时,甲离A地的距离是__________千米;
(6)当S=28时,乙离开A地的时间是__________时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com