【题目】计算（x﹣1）（﹣x﹣1）的结果是（ ）
A.﹣x2+1
B.x2﹣1
C.﹣x2﹣1
D.x2+1
科目：初中数学 来源： 题型：
【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目，希望通过节目的播出，能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛，每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果，按听写正确的汉字个数x绘制成了以下不完整的统计图.
根据以上信息回答下列问题：
（1）本次共随机抽取了_______名学生进行调查，听写正确的汉字个数x在_____________范围内的人数最多；
（2）补全频数分布直方图；
（3）各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数，求被调查学生听写正确的汉字个数的平均数；
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
（4）该校共有1350名学生，如果听写正确的汉字个数不少于21个定为良好，请你估计该校本次“汉字听写”比赛达到良好的学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
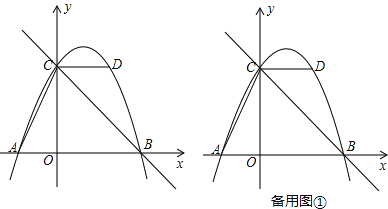
【题目】如图，抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC，CD．
（1）求抛物线的函数表达式；
（2）E是抛物线上的点，求满足∠ECD=∠ACO的点E的坐标；
（3）点M在y轴上且位于点C上方，点N在直线BC上，点P为第一象限内抛物线上一点，若以点C，M，N，P为顶点的四边形是菱形，求菱形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，如果点A，点C为某个菱形的一组对角的顶点，且点A，C在直线y = x上，那么称该菱形为点A，C的“极好菱形”. 下图为点A，C的“极好菱形”的一个示意图.
已知点M的坐标为（1，1），点P的坐标为（3，3）.
（1）点E（2，1），F（1，3），G（4，0）中，能够成为点M，P的“极好菱形”的顶点的是 ；
（2）如果四边形MNPQ是点M，P的“极好菱形”.
①当点N的坐标为（3，1）时，求四边形MNPQ的面积；
②当四边形MNPQ的面积为8，且与直线y = x + b有公共点时，写出b的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
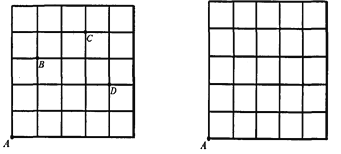
【题目】在边长为1的小正方形组成的网格中，把一个点先沿水平方向平移|a|格（当a为正数时，表示向右平移；当a为负数时，表示向左平移），再沿竖直方向平移|b|格（当b为正数时，表示向上平移；当b为负数时，表示向下平移），得到一个新的点，我们把这个过程记为(a，b)．
例如，从A到B记为：A→B(+l，+3)；从C到D记为：C→D(+1，－2)，
回答下列问题：
（1）如图1，若点A的运动路线为：A→B→C→A，请计算点A运动过的总路程．
（2）若点A运动的路线依次为：A→M(+2，+3)，M→N(+1，－1)，N→P(－2，+2)，P→Q(+4，－4)．请你依次在图2上标出点M、N、P、Q的位置．
（3）在图2中，若点A经过(m，n)得到点E，点E再经过(p，q)后得到Q，则m与p满足的数量关系是 ；n与q满足的数量关系是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列计算中正确的是（ ）
A. (-5)-(-3)=-8 B. (+5)-(-3)=2
C. (-5)-(+3)=-8 D. (-5)-(+3)=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
