
分析 根据分母有理化可以对原始化简,然后再根据平方差公式进行计算即可解答本题.
解答 解:($\frac{2}{{\sqrt{2}+1}}+\frac{2}{{\sqrt{3}+\sqrt{2}}}+\frac{2}{{\sqrt{4}+\sqrt{3}}}+…+\frac{2}{{\sqrt{2002}+\sqrt{2001}}}$)•($\sqrt{2002}$+1)
=$[2(\sqrt{2}-1)+2(\sqrt{3}-\sqrt{2})+2(\sqrt{4}-\sqrt{3})+…+2(\sqrt{2002}-\sqrt{2001})]•(\sqrt{2002}+1)$
=2[$\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+…+\sqrt{2002}-\sqrt{2001}$]$•(\sqrt{2002}+1)$
=2$(\sqrt{2002}-1)(\sqrt{2002}+1)$
=2×(2002-1)
=2×2001
=4002,
故答案为:4002.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:选择题
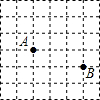 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )| A. | 9个 | B. | 8个 | C. | 7个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 436×104 | B. | 4.36×105 | C. | 4.36×106 | D. | 4.36×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
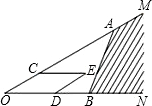 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
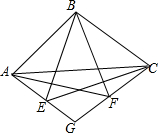 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )| A. | ①②③ | B. | ①②③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com