
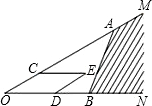
 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 首先延长CE交AB于点F,设OA=a,OB=b,由以OC、OD为邻边作平行四边形OCED,易得△ACF∽△AOB,然后分别求出CF的长,又由CE=OD,比较大小,即可得能否使点E落在阴影区域内.
解答 解:
延长CE交AB于点F,设OA=a,OB=b,
①取OC=$\frac{3}{4}$OA,OD=$\frac{3}{5}$OB,即OC=$\frac{3}{4}$a,OD=$\frac{3}{5}$b,
∴$\frac{AC}{OA}=\frac{CE}{OB}$,
∵OC=$\frac{3}{4}$a,
∴AC=$\frac{1}{4}$a,解得CE=$\frac{1}{4}$b,CE=OD=$\frac{3}{5}$OB=$\frac{3}{5}$b,
∴能使点E落在阴影区域内,
故①正确;
∵四边形ABCD是平行四边形,
∴CE∥OD,
∴△ACF∽△AOB,
∴$\frac{AC}{AO}=\frac{CF}{OB}$,
即CF=$\frac{AC•OB}{OA}$,
取OC=$\frac{3}{4}$OA,OD=$\frac{1}{5}$OB;
即OC=$\frac{3}{4}$a,OD=$\frac{1}{5}$b,
∴AC=$\frac{1}{4}$a,
∴CF=$\frac{1}{4}$b,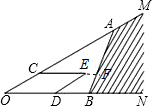
∵CE=OD=$\frac{1}{5}$b,
∴不能使点E落在阴影区域内,
故②错误;
若OC=$\frac{2}{3}$OA,OD=$\frac{4}{5}$OB,则OC=$\frac{2}{3}$a,OD=$\frac{4}{5}$b,
∴AC=$\frac{1}{3}$a,
∴CF=$\frac{1}{3}$b,
∵CE=OD=$\frac{4}{5}$b,
不能使点E落在阴影区域内,
故③错误.
故选B.
点评 解答此题的关键是熟知平行四边形的性质,即三角形相似的性质,两三角形相似其相似比等于各边的比的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | B. | 旅客上飞机前的安检 | ||
| C. | 学校招聘教师,对应聘人员面试 | D. | 了解一批灯泡的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.
如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com