
分析 根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-1≥0}\\{1-x≥0}\end{array}\right.$,解不等式组可得x=1,进而可得y$<\frac{1}{2}$,再根据绝对值的性质可得1-y>0,然后化简约分即可.
解答 解:由题意得:$\left\{\begin{array}{l}{x-1≥0}\\{1-x≥0}\end{array}\right.$,
解得:x=1,
则y$<\frac{1}{2}$,
$\frac{|1-y|}{y-1}$=$\frac{1-y}{y-1}$=-1,
故答案为:-1.
点评 此题主要考查了二次根式有意义的条件,以及绝对值的性质,关键是掌握二次根式中的被开方数是非负数.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
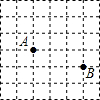 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )| A. | 9个 | B. | 8个 | C. | 7个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 436×104 | B. | 4.36×105 | C. | 4.36×106 | D. | 4.36×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
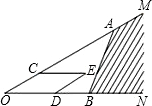 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com