
 如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.
如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.分析 (1)根据路程=速度×时间得出DE=3t,则AE=AD-DE=a-3t,再根据S△ABE=$\frac{1}{2}$AE•AB,代入数据即可求出S=$\frac{1}{2}$ab-$\frac{3}{2}$bt;
(2)将t=1,S=10;t=2,S=4分别代入(1)中所求解析式,得出关于a、b的方程组,求解即可求出a和b的值;
(3)由(2)可得S=16-6t,将t=0.5代入计算即可求解.
解答 解:(1)∵点E在AD上以每秒3个单位的速度从D运动到A,AD=a,
∴DE=3t,AE=AD-DE=a-3t,
∴S△ABE=$\frac{1}{2}$AE•AB=$\frac{1}{2}$(a-3t)•b=$\frac{1}{2}$ab-$\frac{3}{2}$bt,
即S=$\frac{1}{2}$ab-$\frac{3}{2}$bt;
(2)∵当运动时间为1秒时,△ABE的面积为10,
∴$\frac{1}{2}$ab-$\frac{3}{2}$b=10,
∵当运动时间为2秒时,△ABE的面积为4,
∴$\frac{1}{2}$ab-3b=4.
解方程组$\left\{\begin{array}{l}{\frac{1}{2}ab-\frac{3}{2}b=10}\\{\frac{1}{2}ab-3b=4}\end{array}\right.$,得$\left\{\begin{array}{l}{a=8}\\{b=4}\end{array}\right.$,
即a的值为8,b的值为4;
(3)∵a=8,b=4,
∴S=$\frac{1}{2}$×8×4-$\frac{3}{2}$×4t,即S=16-6t,
运动时间为0.5秒时,将t=0.5代入S=16-6t,
得S=16-6×0.5=13.
即△ABE的面积为13.
点评 本题是四边形综合题,其中涉及到路程、速度与时间关系的应用,三角形的面积,求函数解析式以及代数式求值.用含a,b,t的式子正确表示出S是解题的关键.


科目:初中数学 来源: 题型:选择题
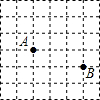 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )| A. | 9个 | B. | 8个 | C. | 7个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
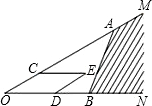 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
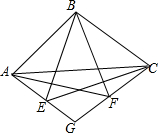 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )| A. | ①②③ | B. | ①②③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com