Question

20．已知点C是线段BD上一动点，△ABC和△ECD均是等边三角形，AD与BE交于点O，连接OC，则下列结论中：
①图形中有三对全等三角形，②OC平分∠BOD，③∠BOD=120°，④OB=OA+OC，⑤若BD=20，则AE的最小值为10，正确的结论有（　　）个．

• A． 5个
• B． 4个
• C． 3个
• D． 2个

Answer 1

分析 ①正确．可以证明△ACD≌△BCE，△ACN≌△BCM（ASA），△CDN≌△CME．
②正确．如图1中，作CF⊥OB于F，CH⊥OD于H，只要证明OH=OF即可．
③正确．由∠MAO+∠AMO+∠AOM=180°，∠MBC+∠BMC+∠MCB=180°，因为∠AMO=∠BMC，∠CBM=∠MAO，所以∠AOM=∠MCB=60°，由此即可证明．
④正确．如图2中，在OB上取一点H，使得CH=CO，只要证明△BCH≌△ACO即可．
⑤正确．如图3中，作AG⊥BC于G，FH⊥BD于H，EF⊥AG于F，由AE=$\sqrt{A{F}^{2}+E{F}^{2}}$，当AE∥BD时，AF=0，AE=EF=10，此时AE的值最小．

解答 解：∵△ABC和△CDE均是等边三角形，
∴AC=BC，CD=CE，∠ACB=∠DCE，
∴∠ACB+∠ACE=∠DCE+∠ACE，
即∠ACD=∠BCE，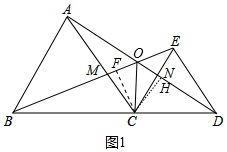
在△ACD和△BCE中，
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$，
∴△ACD≌△BCE（SAS），
∴∠CAD=∠CBE，
在△ACN和△BCM中，
$\left\{\begin{array}{l}{∠ACN=∠BCM}\\{AC=BC}\\{∠CAD=∠CBE}\end{array}\right.$，
∴△ACN≌△BCM（ASA），
∴AN=BM，CM=CN，
同理可证：△CDN≌△CME，
综上所述，①正确，
∵∠MAO+∠AMO+∠AOM=180°，∠MBC+∠BMC+∠MCB=180°，
又∵∠AMO=∠BMC，∠CBM=∠MAO，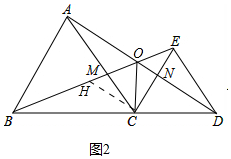
∴∠AOM=∠MCB=60°，
∴∠BOD=120°故③正确，
如图1中，作CF⊥OB于F，CH⊥OD于H，
∵△ACD≌△BCE，
∴AD=BE，
∴S_△ACD=S_△BCE，
∴$\frac{1}{2}$•AD•CH=$\frac{1}{2}$•BE•CF，
∴CF=CH，
∴∠COB=∠COD，故②正确，
如图2中，在OB上取一点H，使得CH=CO，
∵∠COH=60°，
∴△COH是等边三角形，
∴∠CHO=∠OCH=60°，OH=OC，
∵∠BCA=∠HCO，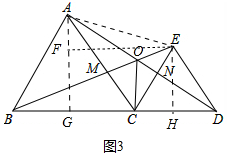
∴∠BCH=∠ACO，∵BC=AC，CH=CO，
∴△BCH≌△ACO，
∴BH=AO，
∴BO=BH+OH=OA+OC，故④正确，
如图3中，作AG⊥BC于G，FH⊥BD于H，EF⊥AG于F，
∵AB=AC，FC=FD，
∴BG=GC，CH=DH，
∴GH=GC+CH=$\frac{1}{2}$（BC+CD）=10，
∵∠EFG=∠FGH=∠GHE=90°，
∴四边形EFGH是矩形，
∴EF=GH=10，
∵AE=$\sqrt{A{F}^{2}+E{F}^{2}}$，
∴当AE∥BD时，AF=0，AE=EF=10，此时AE的值最小，
∴BD=20，则AE的最小值为10，故⑤正确．
综上所述，结论正确的是①②③④⑤共5个
故选A．．

点评 本题考查了全等三角形的判定与性质，等边三角形的性质与判定，角平分线的判定定理，矩形的判定和性质等知识，熟练掌握各性质与判定方法是解题的关键，难点在于需要多次证明三角形全等．