
����Ŀ����ͼ��������ABCD������ƽ���ڣ���A��������A��2��1�����ұ�AB��CD��x��ƽ�У���AD��BC��x��ƽ�У���B��C������ֱ�ΪB��a��1����C��a��c������a��c�����ϵʽ��c=![]() +
+![]() +3
+3
��1����B��C��D��������ꣻ
��2������ƽ�ƣ�����ʹA����ԭ���غϣ�ƽ�ƺ��B��C��D�Ķ�Ӧ�ֱ�ΪB1C1D1 �� ���ı���OB1C1D1�������
��3��ƽ�ƺ���x�����Ƿ���ڵ�P������PD��ʹS��COP=S�ı���OBCD�������������ĵ�P�������P�����ꣻ�������ڣ���˵�����ɣ�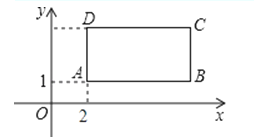
���𰸡��⣺��1��������ã�a��6��0��6��a��0��
���ԣ�a��6��a��6��
���ԣ�a=6��
c=3��
���ԣ���B��6��1����C��6��3����
�߳�����ABCD�ı�AB��CD��x��ƽ�У���AD��BC��x��ƽ�У�
���D��2��3����
��2����ƽ�ƺ�A����ԭ���غϣ�
��ƽ�ƹ���Ϊ����2����λ������1����λ��
��B1��4��0����C1��4��2����D1��0��2����
��3��ƽ�ƺ��C��x��ľ���Ϊ2��
��S��COP=S�ı���OBCD ��
��![]() ��OP��2=4��2��
��OP��2=4��2��
���OP=8��
����P�ڵ�O����ߣ����P������Ϊ����8��0����
����P�ڵ�O���ұߣ����P������Ϊ��8��0����
�������������ڵ�P����8��0����8��0����
����������1�����ݱ��������Ǹ�����ʽ���a��Ȼ�����c�����ɵõ���B��C�����꣬�ٸ��ݾ��ε����ʣ���D�ĺ��������A�ĺ�������ͬ�����������C����������ͬ��
��2�����ݵ�A������ȷ����ƽ�ƹ��ɣ�Ȼ������д��B1��C1��D1�����꣬�����ݾ��ε������ʽ��ʽ���㼴�ɵý⣻
��3�����������ε������ʽ��ʽ���OP���ٷֵ�P�ڵ�O��������ұ����������⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij��˾�����βɹ���һ�����⣬��һ�λ���40��Ԫ���ڶ��λ���60��Ԫ����֪��һ�βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸�������500Ԫ���ڶ��βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸��½���500Ԫ���ڶ��βɹ��������ǵ�һ�βɹ�����������.
��1������ȥ��ÿ�ִ����ƽ���۸��Ƕ���Ԫ��
��2���ù�˾�ɽ�����ӹ�����ۻ���Ƭ���������ӹ�����ۣ�ÿ��ɼӹ�8�ִ��⣬ÿ�ִ������1000Ԫ���������ӹ�����Ƭ��ÿ��ɼӹ�12�ִ��⣬ÿ�ִ������600Ԫ.Ϊ������Ҫ�����вɹ��Ĵ��������30���ڼӹ���ϣ��Ҽӹ���۵Ĵ������������ڼӹ���Ƭ�Ĵ���������һ��.Ϊ����������Ӧ�����ٶִ���ӹ�����ۣ��������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������֪�������ܻ���Ψһ�ġ�ABC����(����)
A. AB��3��BC��4��CA��8 B. AB��4��BC��3����A��30��
C. ��A��35�㣬��B��65�㣬AB��7 D. ��C��90�㣬AB��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ��������( )
A. ƽ���ı��μ�����Գ�ͼ�Σ��������ĶԳ�ͼ��
B. ͬ��(��Ƚ�)��������
C. �߶δ�ֱƽ�����ϵĵ㵽�߶����˵ľ������
D. �����εĶԽ�����ȣ��һ��ഹֱƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У������ȤС���ѧ�������Լ��ռ��ı걾����������Ա������һ����ȫ�黥��182�������ȫ����x��ͬѧ������������г��ķ����ǣ� ��
A.x��x+1��=182
B.x��x��1��=182
C.2x��x+1��=182
D.x��x��1��=182��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�A��B��M��ʾ�����ֱ���a��2a��9����MΪ�߶�AB���е㣬��a��ֵ�ǣ� ��
A. 3B. 4.5C. 6D. 18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����·������·��ֲ��ʱ��ֻҪ�����������ӵ�λ�ã�����ʹͬһ��������һ��ֱ���ϣ���������������___________________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com