
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.AC=DC,∠B=∠E
D.∠B=∠E,∠BCE=∠ACD
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=80°,∠C=40°,
(1)尺规作图:作AC的垂直平分线,交AC于点D,交BC于点E;
(2)连接AE,求证:AB=AE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片![]() 和
和![]() .将这两张三角形胶片的顶点B与顶点E重合,把
.将这两张三角形胶片的顶点B与顶点E重合,把![]() 绕点B顺时针方向旋转,这时AC与DF相交于点O.
绕点B顺时针方向旋转,这时AC与DF相交于点O.
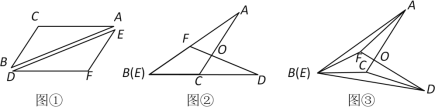
(1)当![]() 旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当![]() 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB=CD=5,BC=AD=3.

(1)如图①,E、F分别为CD、AB边上的点,将矩形ABCD沿EF翻折,使点A与点C重合,设CE=x,则DE= (用含x的代数式表示),CD′=AD=3,在Rt△CD′E中,利用勾股定理列方程,可求得CE= .
(2)如图②,将△ABD沿BD翻折至△A′BD,若A′B交CD于点E,求此时CE的长;
(3)如图③,P为AD边上的一点,将△ABP沿BP翻折至△A′BP,A′B、A′P分别交CD边于E.F,且DF=A′F,请直接写出此时CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论错误的是
A. 全等三角形对应边上的中线相等
B. 两个直角三角形中,两个锐角相等,则这两个三角形全等
C. 全等三角形对应边上的高相等
D. 两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)将△ABC沿y轴翻折,则翻折后点A的对应点的坐标是 .
(2)作出△ABC关于x轴对称的图形△A1B1C1,画△A1B1C1,并直接写出点A1的坐标.
(3)若△DBC与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出了2个小正方形(如图①),其中,3个正方形围成的三角形是直角三角形.再经过一次“生长”后,又生出了4个小正方形(如图②),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”,在“生长”了2019次后形成的图形中所有正方形的面积和是( )

A.2018B.2019C.2020D.2021
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com