
【题目】如图所示,在矩形ABCD中,AB=CD=5,BC=AD=3.

(1)如图①,E、F分别为CD、AB边上的点,将矩形ABCD沿EF翻折,使点A与点C重合,设CE=x,则DE= (用含x的代数式表示),CD′=AD=3,在Rt△CD′E中,利用勾股定理列方程,可求得CE= .
(2)如图②,将△ABD沿BD翻折至△A′BD,若A′B交CD于点E,求此时CE的长;
(3)如图③,P为AD边上的一点,将△ABP沿BP翻折至△A′BP,A′B、A′P分别交CD边于E.F,且DF=A′F,请直接写出此时CE的长.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)![]() 可得表达式,由折叠可得
可得表达式,由折叠可得![]() ,然后用勾股定理列方程求解;
,然后用勾股定理列方程求解;
(2)首先证明DE=EB,设DE=EB=y,在Rt△BEC中,利用勾股定理构建方程即可解决问题;
(3)如图③中,设![]() .首先证明△DFP≌△A′FE,推出
.首先证明△DFP≌△A′FE,推出![]() ,
,![]() ,由
,由![]() ,推出
,推出![]() ,
,![]() ,
,![]() ,在Rt△ECB中,可得
,在Rt△ECB中,可得![]() ,解方程即可.
,解方程即可.
解:(1)![]() ,由折叠可得
,由折叠可得![]() ,
,![]()
在![]() 中,
中,![]()
即![]() ,解得
,解得![]()
(2)如图②中,

∵四边形ABCD是矩形,
∴AB∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴DE=EB,设CE =y,则DE=EB=5y,
在Rt△BEC中,![]() ,
,
(3)如图③中,设PA=PA′=m.

在△DFP和△A′FE中,

∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在Rt△ECB中,![]() ,
,
解得![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠EB.BC=EC,AC=DC
C.BC=DC,∠A=∠DD.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,为了躲避海盗,一轮船一直由西向东航行,早上8点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,10点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行?

查看答案和解析>>
科目:初中数学 来源: 题型:
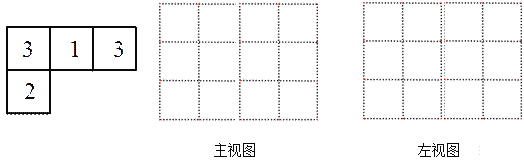
【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
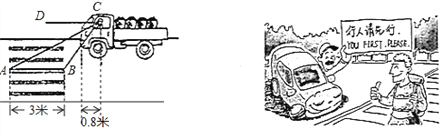
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.AC=DC,∠B=∠E
D.∠B=∠E,∠BCE=∠ACD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8。点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动。它们的运动时间为t(s).


(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变。设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com