
【题目】将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片![]() 和
和![]() .将这两张三角形胶片的顶点B与顶点E重合,把
.将这两张三角形胶片的顶点B与顶点E重合,把![]() 绕点B顺时针方向旋转,这时AC与DF相交于点O.
绕点B顺时针方向旋转,这时AC与DF相交于点O.
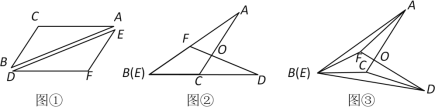
(1)当![]() 旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当![]() 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明.
【答案】(1)∠AFD=∠DCA(或相等);(2)∠AFD=∠DCA(或成立);(3)BO⊥AD.
【解析】
(1)要证∠AFD=∠DCA,只需证△ABC≌△DEF即可;
(2)结论成立,先证△ABC≌△DEF,再证△ABF≌△DEC,得∠BAF=∠EDC,推出∠AFD=∠DCA;
(3)BO⊥AD,由△ABC≌△DEF得BA=BD,点B在AD的垂直平分线上,且∠BAD=∠BDA,继而证得∠OAD=∠ODA,OA=OD,点O在AD的垂直平分线上,即BO⊥AD.
(1)∠AFD=∠DCA.证明如下:
∵AB=DE,BC=EF,∠ABC=∠DEF,∴△ABC≌△DEF,∴∠ACB=∠DFE,∴∠AFD=∠DCA;
(2)∠AFD=∠DCA(或成立),理由如下:
由(1)得:△ABC≌△DEF,∴AB=DE,BC=EF,∠ABC=∠DEF,∠BAC=∠EDF,∴∠ABC﹣∠CBF=∠DEF﹣∠CBF,∴∠ABF=∠DEC.
在△ABF和△DEC中,∵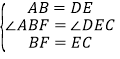 ,∴△ABF≌△DEC(SAS),∠BAF=∠EDC,∴∠BAC﹣∠BAF=∠EDF﹣∠EDC,即∠FAC=∠CDF.
,∴△ABF≌△DEC(SAS),∠BAF=∠EDC,∴∠BAC﹣∠BAF=∠EDF﹣∠EDC,即∠FAC=∠CDF.
∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA,∴∠AFD=∠DCA;
(3)如图,BO⊥AD.证明如下:
由△ABC≌△DEF,点B与点E重合,得∠BAC=∠BDF,BA=BD,∴点B在AD的垂直平分线上,且∠BAD=∠BDA.
∵∠OAD=∠BAD﹣∠BAC,∠ODA=∠BDA﹣∠BDF,∴∠OAD=∠ODA,∴OA=OD,点O在AD的垂直平分线上,∴直线BO是AD的垂直平分线,即BO⊥AD.


科目:初中数学 来源: 题型:
【题目】如图①,点![]() ,
,![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,若
,若![]() .
.

(1)求证:![]() .
.
(2)若将![]() 的边
的边![]() 沿
沿![]() 方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由.
方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算![]() (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算![]() .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
两边同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓广应用:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
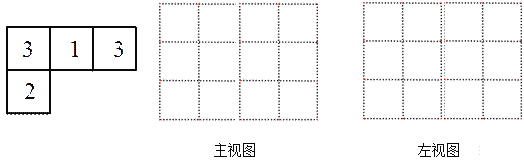
【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).
(1)请在图中画出△AOB关于y轴的对称△A′OB′,点A′的坐标为 ,点B′的坐标为 ;
(2)请写出A′点关于x轴的对称点A′'的坐标为 ;
(3)求△A′OB′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.AC=DC,∠B=∠E
D.∠B=∠E,∠BCE=∠ACD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)

查看答案和解析>>
科目:初中数学 来源: 题型:
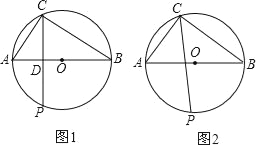
【题目】(已知:如图,AB为⊙O的直径,AC、BC为弦,点P为![]() 上一点,AB=10,AC:BC=3:4.
上一点,AB=10,AC:BC=3:4.
(1)当点P与点C关于直线AB对称时(如图1),求PC的长;
(2)当点P为![]() 的中点时(如图2),求PC的长.
的中点时(如图2),求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com