
【题目】满足下列条件的△ABC不是直角三角形的是( )
A. BC=1,AC=2,AB=![]() ; B. BC:AC:AB=3:4:5
; B. BC:AC:AB=3:4:5
C. ∠A+∠B=∠C D. ∠A:∠B:∠C=3:4:5
【答案】D
【解析】试题分析:根据勾股定理的逆定理可判定A、B,由三角形内角和可判定C、D,可得:
A、当BC=1,AC=2,AB=![]() 时,满足BC2+AB2=1+3=4=AC2,所以△ABC为直角三角形;
时,满足BC2+AB2=1+3=4=AC2,所以△ABC为直角三角形;
B、当BC:AC:AB=3:4:5时,设BC=3x,AC=4x,AB=5x,满足BC2+AC2=AB2,所以△ABC为直角三角形;
C、当∠A+∠B=∠C时,且∠A+∠B+∠C=90°,所以∠C=90°,所以△ABC为直角三角形;
D、当∠A:∠B:∠C=3:4:5时,可设∠A=3x°,∠B=4x°,∠C=5x°,由三角形内角和定理可得3x+4x+5x=180,解得x=15°,所以∠A=45°,∠B=60°,∠C=75°,所以△ABC为锐角三角形.故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
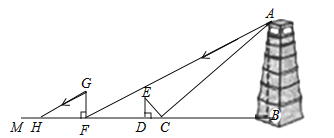
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华盛印染厂生产某种产品,每件产品出厂价为30元,成本价为20元(不含污水处理部分费用).在生产过程中,平均每生产1件产品就有0.5立方米污水排出,所以为了净化环境,工厂设计了两种对污水进行处理的方案并准备实施.
方案一:工厂污水先净化处理后再排出,每处理1立方米污水所用的原料费用为2元,并且每月排污设备损耗等其它各项开支为27000元.
方案二:将污水排放到污水处理厂统一处理,每处理1立方米污水需付8元排污费.
(1)若实施方案一,为了确保印染厂有利润,则每月的产量应该满足怎样的条件?
(2)你认为该工厂应如何选择污水处理方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
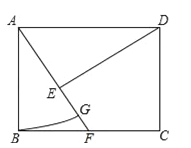
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=![]() ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( )

A.![]() B.4 C.
B.4 C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,8),B(4,0),AB的垂直平分线交y轴与点D,连接BD,M(a,1)为第一象限内的点
(1)则D(____, ____),并求直线BD的解析式;
(2)当![]() 时,求a的值;
时,求a的值;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
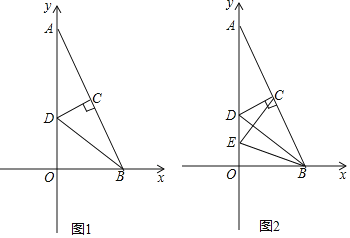
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
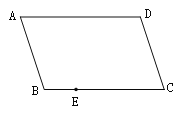
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C这三个点,请回答:

(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com