
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F. 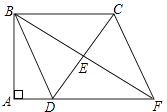
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
【答案】
(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
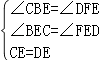 ,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)解:①BC=BD=3时,由勾股定理得,AB= ![]() =
= ![]() =2
=2 ![]() ,
,
所以,四边形BDFC的面积=3×2 ![]() =6
=6 ![]() ;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG=
;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG= ![]() =
= ![]() =
= ![]() ,所以,四边形BDFC的面积=3×
,所以,四边形BDFC的面积=3× ![]() =3
=3 ![]() ;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6
;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6 ![]() 或3
或3 ![]() .
.
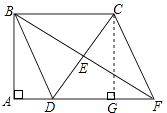
【解析】(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;(2)分①BC=BD时,利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得解;②BC=CD时,过点C作CG⊥AF于G,判断出四边形AGCB是矩形,再根据矩形的对边相等可得AG=BC=3,然后求出DG=2,利用勾股定理列式求出CG,然后利用平行四边形的面积列式计算即可得解;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.


科目:初中数学 来源: 题型:
【题目】A,B两地相距l 100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇,设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:
(1)甲的行进速度为每分钟__________米,m =____分钟;
(2)求直线PQ对应的函数表达式;
(3)求乙的行进速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
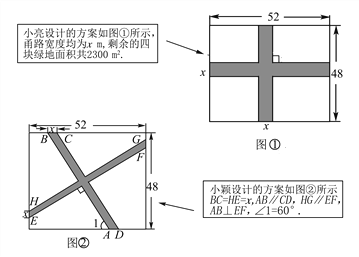
【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指每立方米大气中直径小于或等于0.000 0025米的颗粒粉尘,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害,将0.000 0025米用科学记数法表示为___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论. 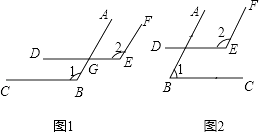
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由:;
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由: .
(3)由(1)(2)你得出的结论是:如果 , 那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com