
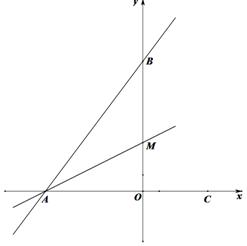
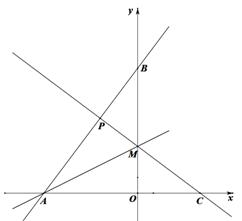
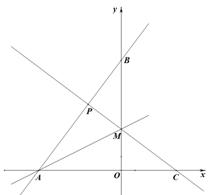
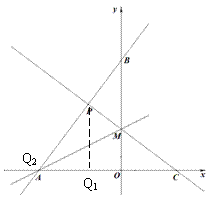
如图,A.B两点的坐标分别是(-6,0),(0,8),M是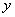 轴上一点,沿AM折叠直线AB刚好落在
轴上一点,沿AM折叠直线AB刚好落在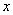 轴上,点B落在点C处.
轴上,点B落在点C处.
(1)直接写出点C的坐标及直线AB的函数关系式;(3分)
(2)求OM的长(请添加适当的辅助线);(3分)
(3)若点P是直线MC与直线AB的交点,请求出点P的坐标;在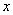 轴上找一点Q,使得以P、Q、C为顶点的三角形是直角三角形(请直接写出Q点坐标).(4分)
轴上找一点Q,使得以P、Q、C为顶点的三角形是直角三角形(请直接写出Q点坐标).(4分)
 |
解:(1)C(4,0) (1分)
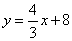 (3分)
(3分)
(2)过点M作DM⊥AB于点D.
设OM为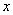
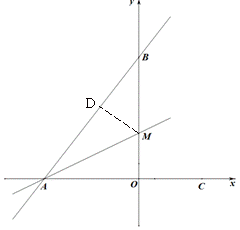
 对折
对折  △ADM≌△AOM
△ADM≌△AOM
 DM=OM=
DM=OM=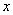 ,AD=AO=6
,AD=AO=6
 BD=10-6=4,BM=8-
BD=10-6=4,BM=8-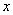 (4分)
(4分)
在Rt△BDM中,由勾股定理得

即 
解得: 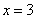 (6分)
(6分)
 OM=3
OM=3
(3)设直线MC的函数关系式 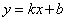 (
(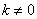 )
)
将M(0,3),C(4,0),代入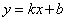 中 ,得
中 ,得
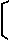
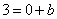

解得: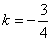 ,
,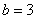
 直线MC的函数关系式为
直线MC的函数关系式为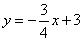 .
.
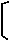

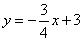
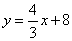
解得: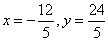
 P(
P(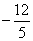 ,
,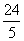 )
)
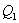 (
(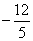 ,0)
,0)  (-6,0)
(-6,0)
 提示:(1)若∠PQC=90° 则
提示:(1)若∠PQC=90° 则 (
(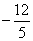 ,0)
,0)
(2)∠PCQ=90°不存在
(3)若∠QPC=90°
解法一:证明△APC≌△AOB从而得出Q点与A点重合,所以 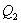 (-6,0).
(-6,0).
解法二:利用勾股定理的逆定理来求
设为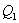
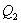 为
为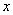 则
则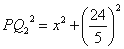 ,
,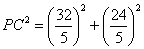
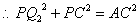
即 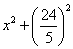 +
+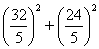 =
=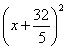
解得: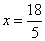 即
即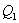
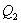 =
=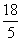

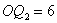

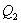 (-6,0)
(-6,0)


科目:初中数学 来源: 题型:
某种商品的进价为800元,出售时标价为1200元,后来由于商品积压,商品准备打折出售,但要保证利润率不低于5 %,则至多可打( )
%,则至多可打( )
A.6折 B.7折 C.8折 D.9折
查看答案和解析>>
科目:初中数学 来源: 题型:
某宾馆底层客房比二楼少5间,某旅行团有48人.若全部住底层,每间4人,房间不够;每间住5人,有房间没 有住满5人.若全部安排在二楼,每间住3人,房间不够;每间住4人,有房间没有住满4人.问该宾馆底层有客房多少间?
有住满5人.若全部安排在二楼,每间住3人,房间不够;每间住4人,有房间没有住满4人.问该宾馆底层有客房多少间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com