练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（　　）
    A．1B．1.5C．2D．2.5

    分析 利用勾股定理求出BC=4，设BE=x，则CE=4-x，在Rt△B'EC中，利用勾股定理解出x的值即可．

    解答 解：BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4，
    由折叠的性质得：BE=BE′，AB=AB′，
    设BE=x，则B′E=x，CE=4-x，B′C=AC-AB′=AC-AB=2，
    在Rt△B′EC中，B′E2+B′C2=EC2，
    即x2+22=（4-x）2，
    解得：x=1.5．
    故选B．

    点评 本题考查了翻折变换的知识，解答本题的关键是掌握翻折变换的性质及勾股定理的表达式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

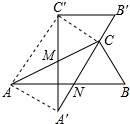    3．有两个全等的含30°角的直角三角板重叠在一起，如图，将△A′B′C′绕AC的中点M转动，斜边A′B′刚好过△ABC的直角顶点C，且与△ABC的斜边AB交于点N，连接AA′、C′C、AC′．若AC的长为2，有以下五个结论：①AA′=1；②C′C⊥A′B′；③点N是边AB的中点；④四边形AA′CC′为矩形；⑤A′N=B′C=$\frac{1}{2}$，其中正确的有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图所示，已知线段a、b、h（h＜b）．求作△ABC，使BC=a，AB=b，BC边上的高AD=h．（要求：写出作法，并保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，已知线段a，b，∠α，按要求完成下列各小题（保留作图痕迹，不要求写作法）
    （1）求作△ABC，使AB=a，BC=b，∠B=∠α，并在BC上找一点D，使得BD=AB，连接AD；
    （2）在（1）的基础上，△ABD的内部是否有到∠C的两边距离相等的点？如果有，有几个？
    （3）在（1）的基础上，△ACD的内部是否有到∠B的两边和∠DAC的两边距离相等的点？如果有，请画出来；如果没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB为x米，面积为y平方米．
    （1）求y与x之间的函数关系式；
    （2）当x取何值时所围成的花圃的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

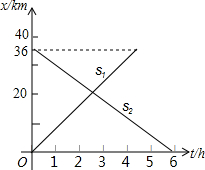    18．如图，甲、乙两人分别从A、B两地同时出发，相向而行．他们各自离A地的路程s1（km）、s2（km）与出发后的时间t（h）之间的函数关系如图7所示，结合图象回答下列问题：
    （1）A、B两地的路程是36km，甲、乙行驶全程所用的时间分别为4.5h和6h；
    （2）求甲、乙两人离A地的路程s1（km）、s2（km）与行驶时间t（h）之间的函数关系式；
    （3）求图象交点的坐标，并解释交点的横坐标和纵坐标所表示的实际意义．
    （4）求两直线与横轴围成的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

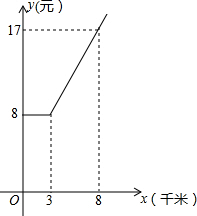    5．如图是某出租车单程收费y（元）与行驶路程x（千米）之间的函数关系图，根据图象回答下列问题：
    （1）当出租车行使2千米时，收费应为8元；当出租车行使8千米时，收费应为17元．
    （2）当出租车行使6千米时，收费应为$\frac{67}{5}$元；当收费为9.4元，出租车行使$\frac{34}{9}$千米．
    （3）请写当x≥3时，出租车收费y（元）与行使路程x（千米）之间的函数关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．为了加强公民的节水意识，合理利用水资源，某城市规定用水收费标准如下：每户每月用水量不超过6m3，水费按按0.6元/m3；每户每月用水量超过6m3时，超过的部分按1元/m3收费．设每户每月用水量为xm3，应缴费为y元．
    （1）写出每月用水量不超过6m3和超过6m3时，y与x之间函数关系式，并判断它们是否为一次函数；
    （2）已知某户5月份的用水量为8m3，求该户5月份应交的水费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）计算：（$\frac{1}{3}$）-2+（π-2014）0+sin60°+$\sqrt{12}$
    （2）先化简，再求值：a（a-3b）+（a+b）2-a（a-b），其中a=1，b=-2．

    查看答案和解析>>

    同步练习册答案