
【题目】如图1,抛物线y=ax2﹣2x﹣3与x轴交于点A、B(3,0),交y轴于点C
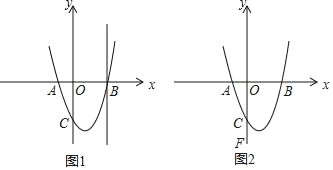
(1)求a的值.
(2)过点B的直线1与(1)中的抛物线有且只有一个公共点,则直线1的解析式为 .
(3)如图2,已知F(0,﹣7),过点F的直线m:y=kx﹣7与抛物线y=x2﹣2x﹣3交于M、N两点,当S△CMN=4时,求k的值.
【答案】(1)a=1;(2)直线的表达式为:x=3或y=4x﹣12;(3)k=﹣2±2![]() .
.
【解析】
(1)把(3,0)代入y=ax2﹣2x﹣3,即可求解;
(2)当直线与y轴平行时,直线l的解析式为:x=﹣3;当直线与y轴不平行时,设:直线1的解析式为:y=kx+b,由△=0即可求解;
(3)联立![]() 得:x2﹣(2+k)x+4=0,由S△CMN=|S△CFN﹣S△CFM|=
得:x2﹣(2+k)x+4=0,由S△CMN=|S△CFN﹣S△CFM|=![]() ×CF×|xM﹣xN|=4,即可求解.
×CF×|xM﹣xN|=4,即可求解.
解:(1)把(3,0)代入y=ax2﹣2x﹣3,
得:0=9a﹣6﹣3,∴a=1;
(2)当直线与y轴平行时,直线l的解析式为:x=﹣3
当直线与y轴不平行时,设:直线1的解析式为:y=kx+b,
将点B坐标代入上式,解得:b=﹣3k
则直线的表达式为:y=kx﹣3k…①,
抛物线的表达式为:y=x2﹣2x﹣3…②,
联立①②并整理得:x2﹣(k+2)x+(3k﹣3)=0,
△=b2﹣4ac=(k+2)2﹣4(3k﹣3)=0,
解得:k=4,
故:直线的表达式为:x=3或y=4x﹣12;
(3)联立![]() 得:x2﹣(2+k)x+4=0,
得:x2﹣(2+k)x+4=0,
xM+xN=k+2,xMxN=4,
∵S△CMN=|S△CFN﹣S△CFM|=![]() ×CF×|xM﹣xN|=4,
×CF×|xM﹣xN|=4,
∴![]() ×4×
×4×![]() =4,
=4,
即:(k+2)2=20,
解得:k=﹣2±2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校课程中心为了了解学生对开设的3D打印、木工制作、机器人和电脑编程四门课程的喜爱程度,随机调查了部分学生,每人只能选一项最喜爱的课程.图①是四门课程最喜爱人数的扇形统计图,图②是四门课程男、女生最喜爱人数的条形统计图.
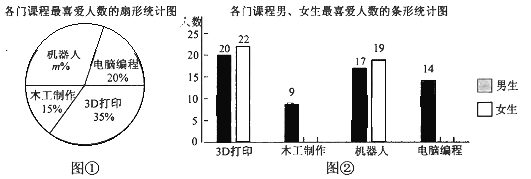
(1)求图①中![]() 的值,补全图②中的条形统计图,标上相应的人数;
的值,补全图②中的条形统计图,标上相应的人数;
(2)若该校共有1800名学生,则该校最喜爱3D打印课程的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
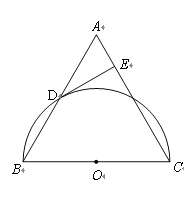
求证:(1)△ABC是等边三角形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市十个全覆盖工作的推动下,某乡镇准备在相距3千米的A、B两个工厂间修一条笔直的公路,在工厂A北偏东60°方向、工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
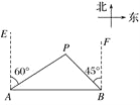
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分) 甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转。
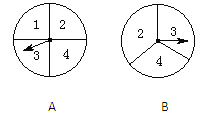
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-4x+3=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-4x+3=0的解时,则乙获胜.问他们两人谁获胜的概率大?请分析说明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在铅直高度为200 m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的点C处测得山顶B的仰角为30°(即∠BCD=300),测得塔顶A的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB(精确到1 m)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com