
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) 
A.π
B.π+5
C.![]()
D.![]()
【答案】D
【解析】解:作DH⊥AE于H, ∵∠AOB=90°,OA=2,OB=1,
∴AB= ![]() =
= ![]() ,
,
由旋转的性质可知,OE=OB=1,DE=EF=AB= ![]() ,△DHE≌△BOA,
,△DHE≌△BOA,
∴DH=OB=1,
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积
= ![]() ×3×1+
×3×1+ ![]() ×1×2+
×1×2+ ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]() π,
π,
故选:D.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2),以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE. 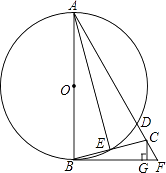
(1)直接写出AE与BC的位置关系;
(2)求证:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形, ![]() 与直径AB交于点C,连接点C与圆心O′.
与直径AB交于点C,连接点C与圆心O′. 
(1)求 ![]() 的长;
的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 .
查看答案和解析>>
科目:初中数学 来源: 题型:
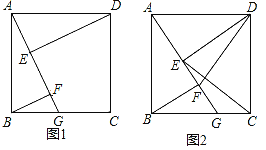
【题目】如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:DE=AF;
(2)若AB=4,BG=3,求AF的长;
(3)如图2,连接DF、CE,判断线段DF与CE的位置关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,有下列结论: ①它的图象与x轴有两个交点;
②如果将它的图象向左平移3个单位后过原点,则m=1;
③如果当x=2时的函数值与x=8时的函数值相等,则m=5.
其中一定正确的结论是 . (把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com