
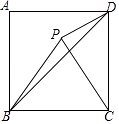
【题目】如图,在正方形ABCD中,△APBC是等边三角形,连接PD,DB,则 ![]() = .
= . 
【答案】![]()
【解析】解:如图, 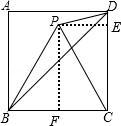
过P作PE⊥CD,PF⊥BC,
设正方形ABCD的边长是啊,
∵△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=a,
∴∠PCE=30°
∴PF=PBsin60°= ![]() a,PE=PCsin30°=
a,PE=PCsin30°= ![]() a,
a,
∴S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD= ![]() ×a×
×a× ![]() a+
a+ ![]() ×
× ![]() a×a﹣
a×a﹣ ![]() ×a×a=
×a×a= ![]() a2 ,
a2 ,
∴ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用等边三角形的性质和正方形的性质,掌握等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


科目:初中数学 来源: 题型:
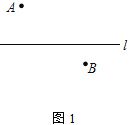
【题目】(1) 如图1,在一条笔直的公路两侧,分别有A、B两个村庄,现在要在公路l旁建一座火力发电厂,向A、B两个村庄供电,为使所用的电线最短,请问供电厂P应健在何处?画出图形,不写作法,保留作图痕迹;
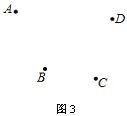
(2) 如图2,若要向4个村庄A、B、C、D供电,供电厂P又该建在何处能使所用电线最短呢?画出图形,不写作法,保留作图痕迹;
(3)A、B、C、D如图3,连接AC并延长到E,使CE=AC,连接BD并反向延长到F,不写作法,保留作图痕迹.
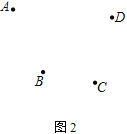
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架5米长的梯子AB斜靠在一面墙上,梯子底端B到墙底的垂直距离BC为3米.
(1)求这个梯子的顶端A到地面的距离AC的值;
(2)如果梯子的顶端A沿墙AC竖直下滑1米到点D处,求梯子的底端B在水平方向滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) 
A.π
B.π+5
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个只允许单向通过的窄道口,通常情况下,每分钟可以通过9人.一天王老师到达道口时,发现由于拥挤,每分钟只能有3人通过道口,此时,自己前面还有36人等待通过(假定先到达的先过,王老师过道口的时间忽略不计),通过道口后,还需7分钟到达学校.

(1)此时,若绕道而行,要15分钟才能到达学校,从节省时间考虑,王老师应选择绕道去学校,还是选择通过拥挤的道口去学校?
(2)若在王老师等人的维持下,几分钟后秩序恢复正常(维持秩序期间,每分钟仍有3人通过道口),结果王老师比在拥挤的情况下提前6分钟通过道口,问维持秩序的时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正确的有( )
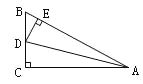
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 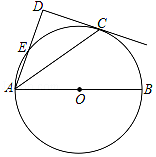
(1)求证:AC平分∠DAB;
(2)连接CE,若CE=6,AC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com