
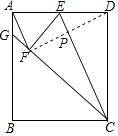
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.
【答案】
(1)
证明:连接FD交EC于P,
由折叠矩形ABCD可得,EF=ED,CF=CD,∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°,
∵点E为AD的中点,
∴AE=ED=EF,
∴∠EAF=∠EFA,
∵∠DEF=∠EAF+∠EFA=∠DEC+∠FEC,
∴∠EAF=∠DEC,
∴AF∥EC;
(2)
∵EF=ED,CF=CD,
∴E,C两点都在线段DF的中垂线上,即EC⊥DF,
∴∠DPE=90°,
∵AF∥EC,
∴∠AFD=∠DPE=∠EDC=90°,
∵∠EAF=∠DEC,∠AFD=∠EDC,
∴△AFD∽△EDC,
∴ ![]() ,即AFEC=DEAD,
,即AFEC=DEAD,
∴AFEC=2EF2;
(3)
∵∠GAF+∠EAF=∠GFA+∠EFA=90°,∠EAF=∠EFA,
∴∠GAF=∠GFA,
∴AG=FG,
在Rt△BGC中,BC=6,BG=8,
CG= ![]() =10,
=10,
∵AB=CD=CF,
∴8+AG=10﹣FG,
∴AG=FG=1,
∴CF=CD=9,
∵AD=BC=6,
∴EF= ![]() AD=3,
AD=3,
∴在Rt△DEC中,EC= ![]() =3
=3 ![]() ,
,
∵AFEC=2EF2,
∴3 ![]() ×AF=2×32,
×AF=2×32,
解得,AF= ![]() .
.
【解析】(1)连接FD交EC于P,根据折叠的性质得到EF=ED,CF=CD,∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°,根据直角三角形的性质得到AE=ED=EF,求出∠EAF=∠DEC,根据平行线的判定定理证明;(2)证明△AFD∽△EDC,根据相似三角形的性质定理计算即可;(3)根据勾股定理求出CG,根据矩形的性质求出AB,根据(2)的结论计算即可.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
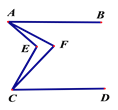
【题目】如图,已知AB‖CD,∠EAF =![]() ∠EAB,∠ECF=
∠EAB,∠ECF=![]() ∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,有下列结论: ①它的图象与x轴有两个交点;
②如果将它的图象向左平移3个单位后过原点,则m=1;
③如果当x=2时的函数值与x=8时的函数值相等,则m=5.
其中一定正确的结论是 . (把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
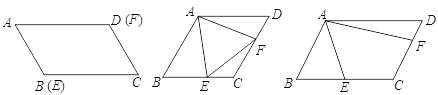
【题目】点E、F分别是□ABCD的边BC、CD上的点,∠EAF=60°,AF=4
(1) 若AB=2,点E与点B、点F与点D分别重合,求平行四边形ABCD的面积
(2) 若AB=BC,∠B=∠EAF=60°,求证:△AEF为等边三角形
(3) 若BE=CE,CF=2DF,AB=3,直接写出AE的长度(无需解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( ) 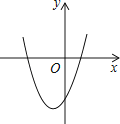
A.y1<y2
B.y1>y2
C.y的最小值是﹣3
D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
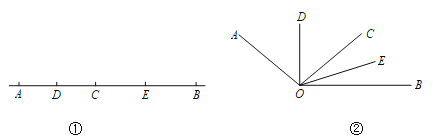
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com