
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 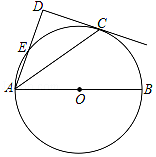
(1)求证:AC平分∠DAB;
(2)连接CE,若CE=6,AC=8,求AE的长.
【答案】
(1)证明:连接OC,如图,
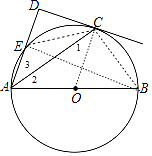
∵CD为切线,
∴OC⊥CD,
又∵AD⊥CD,
∴OC∥AD,
∴∠1=∠3
又∵OA=OC,
∴∠1=∠2,
∴∠2=∠3,
∴AC平分∠DAB
(2)解:连接BC,BE,BE交OC于F,如图,

∵AB为直径,
∴∠AEB=90°,
易得四边形DEFC为矩形,
∴OC⊥BE,
∴ ![]() =
= ![]() ,
,
∴BC=CE=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= ![]() =10,
=10,
∵∠3=∠2,
∴Rt△ADC∽Rt△ACB,
∴AD:AC=AC:AB,
∴AD= ![]() =6.4,
=6.4,
∵∠DEC=∠ABC,
∴Rt△DEC∽Rt△CBA,
∴DE:BC=CE:AB,
∴DE= ![]() =3.6,
=3.6,
∴AE=AD﹣DE=6.4﹣3.6=2.8
【解析】(1)连接OC,如图,根据切线的性质得到OC⊥CD,则可证明OC∥AD,所以∠1=∠3,加上∠1=∠2,于是得到∠2=∠3;(2)连接BC,BE,BE交OC于F,如图,先利用圆周角定理得到∠AEB=90°,易得四边形DEFC为矩形,则OC⊥BE,根据垂径定理得到 ![]() =
= ![]() ,所以BC=CE=6,于是可计算出AB=10,接着证明Rt△ADC∽Rt△ACB,利用相似比计算出AD,证明Rt△DEC∽Rt△CBA,利用相似比计算出DE,然后计算AD﹣DE即可.
,所以BC=CE=6,于是可计算出AB=10,接着证明Rt△ADC∽Rt△ACB,利用相似比计算出AD,证明Rt△DEC∽Rt△CBA,利用相似比计算出DE,然后计算AD﹣DE即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.
查看答案和解析>>
科目:初中数学 来源: 题型:
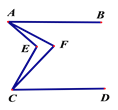
【题目】如图,已知AB‖CD,∠EAF =![]() ∠EAB,∠ECF=
∠EAB,∠ECF=![]() ∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com