
 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )| A. | (-2,4) | B. | (-4,1) | C. | (-3,2) | D. | (-2,1) |
分析 作AE⊥BC于E,由四边形ABCD为平行四边形得AD∥x轴,则可判断四边形ADOE为矩形,所以S平行四边形ABCD=S矩形ADOE,根据反比例函数k的几何意义得到S矩形ADOE=|-k|=4,从而得出k=-4,因为B点的横坐标和纵坐标的积等于-4,即可判断(-4,1)在反比例函数的图象上.
解答 解: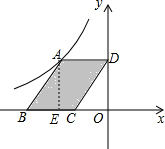 作AE⊥BC于E,如图,
作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD∥x轴,
∴四边形ADOE为矩形,
∴S平行四边形ABCD=S矩形ADOE,
而S矩形ADOE=|-k|,
∴|-k|=4,
而k<0,
∴k=-4.
∵-4×1=-4,
∴点(-4,1)是反比例函数图象上的点,
故选B.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
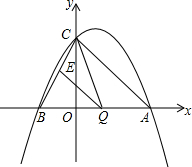 如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.
如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com