练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若a是$\sqrt{15}$-2的整数部分，b为5-$\sqrt{15}$的小数部分，则（$\sqrt{15}$-2）•a+b=2．

    分析 先估算$\sqrt{15}$的范围，再估算$\sqrt{15}$-2，5-$\sqrt{15}$的范围，即可确定a，b的值，即可解答．

    解答 解：∵$3＜\sqrt{15}＜4$，
    ∴$1＜\sqrt{15}-2＜2$，1$＜5-\sqrt{15}＜2$，
    ∴$\sqrt{15}$-2的整数部分为：a=1，
    5-$\sqrt{15}$的小数部分为：b=5-$\sqrt{15}$-1=$4-\sqrt{15}$，
    ∴（$\sqrt{15}$-2）•a+b=（$\sqrt{15}$-2）×1+4-$\sqrt{15}$=$\sqrt{15}$-2+4-$\sqrt{15}$=2，
    故答案为：2．

    点评 本题主要考查了估算无理数的大小，判断出所给的无理数的近似值是解题的关键，是一道较简单的题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图，点A是反比例函数y=$\frac{k}{x}$（x＜0）图象上的一点，过点A作平行四边形ABCD，使点B，C在x轴上，点D在y轴上，S?ABCD=4，则下列点在反比例函数y=$\frac{k}{x}$（x＜0）图象上的是（　　）
    A．（-2，4）B．（-4，1）C．（-3，2）D．（-2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

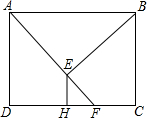    10．如图，矩形ABCD中，F为CD边上一点，AF=AB，BE⊥AF，EH⊥CD垂足分别为点E、H．
    （1）求证：△ADF≌△BEA；
    （2）若AD：AB=3：4，EF=3，求EH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．测定某运动员跑100m的平均速度，测的结果是跑完前24m用了3s，跑完后76m又用了6s，该运动员的平均速度是（　　）
    A．8m/sB．11.1m/sC．12.7m/sD．10.35m/s

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．在函数y=$\sqrt{x-3}$中，自变量x的取值范围是（　　）
    A．x≥3B．x＞3C．x≤3D．x＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简：
    （1）$\frac{（x-y）^2}{xy}$-$\frac{{x}^{2}-{y}^{2}}{xy}$；
    （2）$\frac{{a}^{2}}{a-b}$-$\frac{{b}^{2}}{b-a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．代数式$\frac{a}{|a|}+\frac{|b|}{b}+\frac{ab}{|ab|}$的所有不同的值有（　　）
    A．2个B．3个C．4个D．无数个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

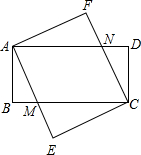    8．已知：如图，四边形ABCD和四边形AECF都是矩形，AE与BC交于点M，CF与AD交于点N．
    （1）求证：△ABM≌△CDN；
    （2）矩形ABCD和矩形AECF满足何种关系时，四边形AMCN是菱形，证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

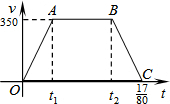    11．京沪高速铁路已开工建设，某校研究性学习以此为课题，在研究列车的行驶速度时，得到一个数学问题．如图，若v是关于t的函数，图象为折线O-A-B-C，其中A（t1，350），B（t2，350），C（$\frac{17}{80}$，0），四边形OABC的面积为70，则t1-t2=（　　）
    A．$\frac{1}{5}$B．$\frac{3}{16}$C．$\frac{7}{80}$D．$\frac{31}{160}$

    查看答案和解析>>

    同步练习册答案