
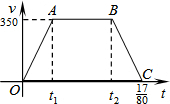
 京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )
京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{16}$ | C. | $\frac{7}{80}$ | D. | $\frac{31}{160}$ |
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )| A. | 64个 | B. | 49个 | C. | 36个 | D. | 25个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com