
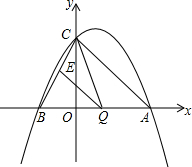
 ��ͼ����֪��������y�ύ�ڵ�C��0��4������x�ύ��A��x1��0����B��x2��0��������x1��x2Ϊ����x2-2x-8=0����������
��ͼ����֪��������y�ύ�ڵ�C��0��4������x�ύ��A��x1��0����B��x2��0��������x1��x2Ϊ����x2-2x-8=0�������������� ��1���������÷������ͼ����x�ύ�����꣬������C������������a��ֵ���ɣ�
��2����EH��AB�ڵ�H���ɵ�EH��CO������QE��AC���ɵó�������ϵ���������EH�ij��ȣ����S��CQE���ó���ϵʽ���������ֵ��
��3�����ڣ����ô���ϵ�������AC�Ľ���ʽ����F��x��-x+4������ʾ��OM��MF��OF�ij��ȣ�Ҫʹ��OMF�ǵ����������������������OF=FMʱ����OM=OF=2ʱ����OM=MFʱ���ֱ������F�����꣮
��� �⣺��1���ⷽ��x2-2x-8=0�ã�x1=4��x2=-2��
��A��4��0����B��-2��0����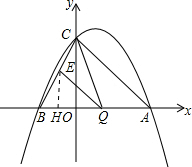
�������߽���ʽΪy=a��x-4����x+2����
��C��0��4�����룬��ã�a=-$\frac{1}{2}$��
�������߽���ʽΪy=-$\frac{1}{2}$x2+x+4��
��2����Q��x��0�����ɵ�BQ=x+2��AQ=4-x��
��EH��AB�ڵ�H��
��EH��CO��
��$\frac{EH}{CO}$=$\frac{BE}{BC}$��
�֡�QE��AC��
��$\frac{BE}{BC}$=$\frac{BQ}{BA}$��
��$\frac{EH}{CO}$=$\frac{BQ}{BA}$��
��$\frac{EH}{4}$=$\frac{x+2}{6}$������EF=$\frac{2}{3}$��x+2����
��S��CQE=S��CBQ-S��EBQ=$\frac{1}{2}$��x+2����4-$\frac{1}{2}$��x+2����$\frac{2}{3}$��x+2����
��y����x�ĺ�����ϵʽΪy=-$\frac{1}{3}$x2+$\frac{2}{3}$x+$\frac{8}{3}$=-$\frac{1}{3}$��x-1��2+3��-2��x��4����
���CQE����������ֵΪ3��
��3�����ڣ��������£�
��AC�Ľ���ʽΪ��y=kx+b��
��AC��A��4��0����C��0��4����
��$\left\{\begin{array}{l}4k+b=0\\ b=4\end{array}\right.$��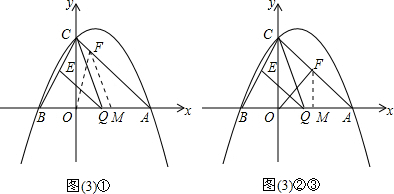
��AC�Ľ���ʽΪ��y=-x+4��
��F��AC�ϣ���F��x��-x+4����
��OF=$\sqrt{{x}^{2}+��-x+4��^{2}}$��MF=$\sqrt{��x-2��^{2}+��-x+4��^{2}}$��OM=2��
����OMF�ǵ��������ο��������������
��OF=FMʱ��F�ĺ�����ӦΪ1��F��1��3������11�֣�
��OM=OF=2ʱ��$\sqrt{{x}^{2}+��-x+4��^{2}}$=2��
����ã�x2-4x+6=0
�ߡ�=-8��0
��������������ڣ�
��OM=MF=2$\sqrt{��x-2��^{2}+��-x+4��^{2}}$=2��
����ã�x2-6x+8=0
��ã�x1=2��x2=4����ȥ��
��F��2��2����
��������������OMF�ǵ���������ʱ��F��1��3����2��2����
���� ���⿼���˶��κ������ۺ�Ӧ�ã��漰�˽��Ԫһ�η��̡�����ϵ������������ʽ�����������ʡ����������ε��ж��������Լ�������κ�����ֵ��֪ʶ�㣬���ڣ�3����ʱ��һ��Ҫע���������۵��������ε�����������©�⣬�����ۺ��Խ�ǿ���ѶȽϴ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A�Ƿ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ�һ�㣬����A��ƽ���ı���ABCD��ʹ��B��C��x���ϣ���D��y���ϣ�S?ABCD=4�������е��ڷ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ��ǣ�������
��ͼ����A�Ƿ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ�һ�㣬����A��ƽ���ı���ABCD��ʹ��B��C��x���ϣ���D��y���ϣ�S?ABCD=4�������е��ڷ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ��ǣ�������| A�� | ��-2��4�� | B�� | ��-4��1�� | C�� | ��-3��2�� | D�� | ��-2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
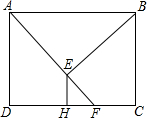 ��ͼ������ABCD�У�FΪCD����һ�㣬AF=AB��BE��AF��EH��CD����ֱ�Ϊ��E��H��
��ͼ������ABCD�У�FΪCD����һ�㣬AF=AB��BE��AF��EH��CD����ֱ�Ϊ��E��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8m/s | B�� | 11.1m/s | C�� | 12.7m/s | D�� | 10.35m/s |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
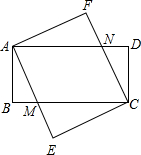 ��֪����ͼ���ı���ABCD���ı���AECF���Ǿ��Σ�AE��BC���ڵ�M��CF��AD���ڵ�N��
��֪����ͼ���ı���ABCD���ı���AECF���Ǿ��Σ�AE��BC���ڵ�M��CF��AD���ڵ�N���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com