练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
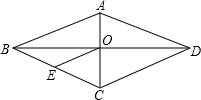
    16．已知：如图，菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD=6cm，则OE的长为（　　）
    A．6cmB．4cmC．3cmD．2cm

    分析 由菱形ABCD中，OE∥DC，可得OE是△BCD的中位线，又由AD=6cm，根据菱形的性质，可得CD=6cm，再利用三角形中位线的性质，即可求得答案．

    解答 解：∵四边形ABCD是菱形，
    ∴CD=AD=6cm，OB=OD，
    ∵OE∥DC，
    ∴BE：CE=BO：DO，
    ∴BE=CE，
    即OE是△BCD的中位线，
    ∴OE=$\frac{1}{2}$CD=3cm．
    故选C．

    点评 此题考查了菱形的性质以及三角形中位线的性质．注意证得OE是△BCD的中位线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．实数a、b、c在数轴上的对应点位置如图．化简：|c|-$\sqrt{（c+a）^{2}}$+$\sqrt{{b}^{2}}$-|a-b|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，数轴上所表示关于x的不等式组的解集是（　　）
    A．x≥2B．x＞2C．x＞-1D．-1＜x≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

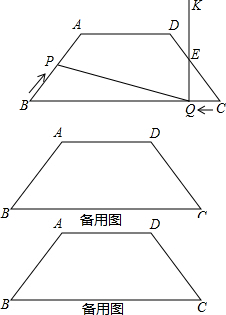    4．如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12，点P从点B出发沿折线段BA-AD-DC以每秒1个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒$\frac{3}{5}$个单位长的速度匀速运动，过点Q向上作射线QK⊥BC，交折线段CD-DA-AB于点E；点P、Q同时开始运动，当点P与点C重合时停止运动，点Q也随之停止，设P、Q运动的时间为t秒（t＞0）．
    （1）当点P运动到AD上时，t为何值时能使PQ∥DC？
    （2）设射线QK扫过梯形ABCD的面积为s，求s与t的函数关系式，并写出t的取值范围．
    （3）在整个运动过程中，△PDQ能否是直角三角形？若能，直接写出此时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

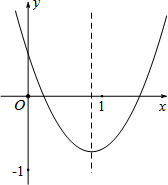    11．已知二次函数y=ax2+bx+c的图象如图所示，则下列7个代数式ab，ac，bc，b2-4ac，a+b+c，a-b+c，2a+b中，其值为正的式子的个数为（　　）
    A．2个B．3个C．4个D．4个以上

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．矩形ABCD的对角线AC=8cm，∠AOD=120°，则CB的长为4$\sqrt{3}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若a+b+c≠0，$\frac{2a+b}{c}$=$\frac{2b+c}{a}$=$\frac{2c+a}{b}$=k，则k=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

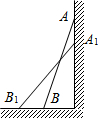    5．如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？
    （1）请你将小明对“思考题”的解答补充完整：
    解：设点B将向外移动x米，即BB1=x，
    则B1C=x+0.7，A1C=AC-AA1=$\sqrt{{2.5}^{2}-{0.7}^{2}}$-0.4=2
    而A1B1=2.5，在Rt△A1B1C中，由B1C2+A1C2=A1B12得方程（x+0.7）2+22=2.52，
    解方程得x1=0.8，x2=-2.2（不合题意舍去），∴点B将向外移动0.8米．
    （2）解完“思考题”后，小聪提出了如下问题：
    梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？请你解答小聪提出的这个问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．学校为了考察我校七年级同学的视力情况，从七年级的10个班共540名学生中，每班抽取了5名进行分析，在这个问题中，总体是540名学生的视力，样本容量是50．

    查看答案和解析>>

    同步练习册答案