
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针得到
顺时针得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
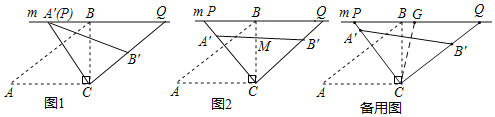
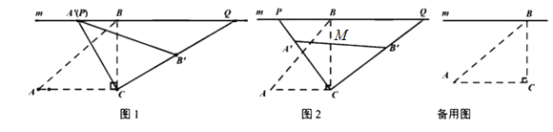 (1)如图1,当
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程时,当点![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
【答案】(1)60°;(2)![]() ;(3)
;(3)![]()
【解析】(1)由旋转可得:AC=A'C=2,进而得到BC=![]() ,依据∠A'BC=90°,可得cos∠A'CB=
,依据∠A'BC=90°,可得cos∠A'CB=![]() ,即可得到∠A'CB=30°,∠ACA'=60°;
,即可得到∠A'CB=30°,∠ACA'=60°;
(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB=![]() BC=
BC=![]() ,依据tan∠Q=tan∠A=
,依据tan∠Q=tan∠A=![]() ,即可得到BQ=BC×
,即可得到BQ=BC×![]() =2,进而得出PQ=PB+BQ=
=2,进而得出PQ=PB+BQ=![]() ;
;
(3)依据S四边形PA'B′Q=S△PCQ-S△A'CB'=S△PCQ-![]() ,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=
,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=![]() PQ×BC=
PQ×BC=![]() PQ,得到S△PCQ的最小值=3,S四边形PA'B′Q=3-
PQ,得到S△PCQ的最小值=3,S四边形PA'B′Q=3-![]() .
.
(1)由旋转可得:AC=A'C=2,
∵∠ACB=90°,AB=![]() ,AC=2,
,AC=2,
∴BC=![]() ,
,
∵∠ACB=90°,m∥AC,
∴∠A'BC=90°,
∴cos∠A'CB=![]() ,
,
∴∠A'CB=30°,
∴∠ACA'=60°;
(2)∵M为A'B'的中点,
∴∠A'CM=∠MA'C,
由旋转可得,∠MA'C=∠A,
∴∠A=∠A'CM,
∴tan∠PCB=tan∠A=![]() ,
,
∴PB=![]() BC=
BC=![]() ,
,
∵tan∠Q=tan∠A=![]() ,
,
∴BQ=BC×![]() =2,
=2,
∴PQ=PB+BQ=![]() ;
;
(3)∵S四边形PA'B′Q=S△PCQ-S△A'CB'=S△PCQ-![]() ,
,
∴S四边形PA'B′Q最小,即S△PCQ最小,
∴S△PCQ=![]() PQ×BC=
PQ×BC=![]() PQ,
PQ,
取PQ的中点G,则∠PCQ=90°,
∴CG=![]() PQ,即PQ=2CG,
PQ,即PQ=2CG,
当CG最小时,PQ最小,
∴CG⊥PQ,即CG与CB重合时,CG最小,
∴CGmin=![]() ,PQmin=2
,PQmin=2![]() ,
,
∴S△PCQ的最小值=3,S四边形PA'B′Q=3-![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,P1、P2是反比例函数y=![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)直接写出反比例函数的解析式.
(2)①求P2的坐标.
②根据图象直接写出在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=![]() 的函数值.
的函数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
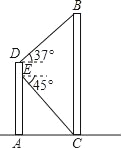
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() ≌
≌![]() .
.
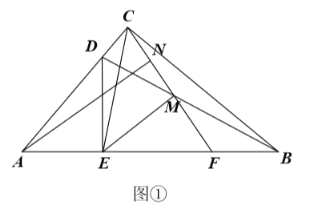
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
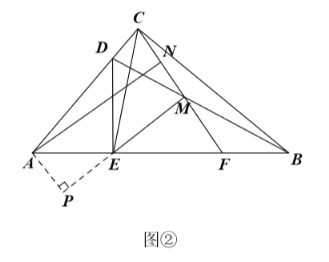
(3)如图②,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题.
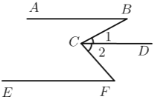
(1)探究:如图,![]() ,试说明
,试说明![]() .
.
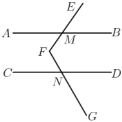
(2)拓展:如图,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,利用探究结论求
,利用探究结论求![]() 的度数.
的度数.
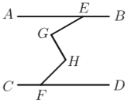
(3)应用:如图,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在
在![]() 与
与![]() 之间,
之间,![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为______度.
的大小为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
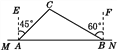
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com