
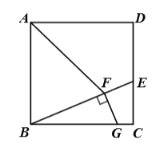
【题目】如图,在正方形![]() 中,
中,![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,且
边上,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A. 10B. 11C. 12D. 13
【答案】D
【解析】
过点A作AH⊥BE于K,交BC于H,设AB=m,由正方形性质和等腰三角形性质可证明:△BKH∽△BFG,BH=![]() BG,再证明△ABH≌△BCE,可得BH=CE,可列方程
BG,再证明△ABH≌△BCE,可得BH=CE,可列方程![]() (m2)=m7,即可求得BC=12,CE=5,由勾股定理可求得BE.
(m2)=m7,即可求得BC=12,CE=5,由勾股定理可求得BE.
解:如图,过点A作AH⊥BE于K,交BC于H,设AB=m,
∵正方形ABCD
∴BC=CD=AB=m,∠ABH=∠C=90°
∵CG=2,DE=7,
∴CE=m7,BG=m2
∵FG⊥BE
∴∠BFG=90°
∵AF=AB,AH⊥BE
∴BK=FK,即BF=2BK,∠BKH=90°=∠BFG
∴△BKH∽△BFG
∴![]() ,即BH=
,即BH=![]() BG=
BG=![]() (m2)
(m2)
∵∠ABK+∠CBE=∠ABK+∠BAH=90°
∴∠BAH=∠CBE
在△ABH和△BCE中,∠BAH=∠CBE,AB=BC,∠ABH=∠BCE,
∴△ABH≌△BCE(ASA)
∴BH=CE
∴![]() (m2)=m7,解得:m=12
(m2)=m7,解得:m=12
∴BC=12,CE=127=5
在Rt△BCE中,BE=![]() .
.
故选:D.


科目:初中数学 来源: 题型:
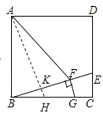
【题目】如图,已知Rt△ABC中,C=90°,O在AC上,以OC为半径作⊙O,切AB于D点,且BC=BD.
(1)求证:AB为⊙O的切线;
(2)若BC=6,sinA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,P点在⊙O上为一动点,求BP的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
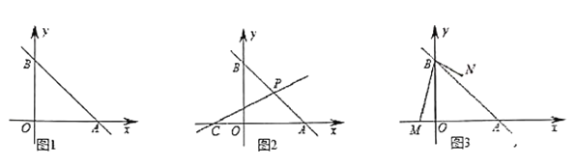
(1)直接写出![]() 的值为______.
的值为______.
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班级为了促进同学养成良好的学习习惯,每天都对同学进行学规管理记分.如下是小李同学第8周学规得分(规定:加分为“+”,扣分为“﹣”).

(1)第8周小李学规得分总计是多少?
(2)根据班规,一学期里班级还会将同学每周的学规得分进行累加.已知小李同学第7周末学规累加分数为98分,若他在第9周末学规累加分数达到105分,则他第9周的学规得分总计是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
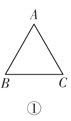
【题目】(1)如图①所示,在△ABC中,∠A+∠B+∠C=___________度;
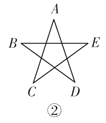
(2)如图②所示,在五角星中,∠A+∠B+∠C+∠D+∠E=__________度;
(3)如图③所示,在七角星中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针得到
顺时针得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
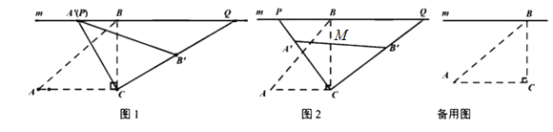 (1)如图1,当
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程时,当点![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
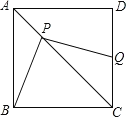
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=![]() ,CQ=3,则四边形PBCQ的面积为_______.
,CQ=3,则四边形PBCQ的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
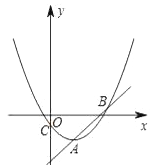
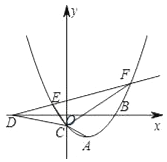
【题目】如图,抛物线![]() (m<0)的顶点为A,交y轴于点C.
(m<0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)平移直线y=x经过点A交抛物线C于另一点B,直线AB下方抛物线C上一点P,求点P到直线AB的最大距离
(3)设直线AC交x轴于点D,直线AC关于x轴对称的直线交抛物线C于E、F两点.若∠ECF=90°,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com