
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
【答案】(1)∠A+∠D=∠C+∠B; (2)有6个;(3)∠P=45°;
【解析】
(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;
(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=50°,∠B=40°,
∴2∠P=50°+40°,
∴∠P=45°;


科目:初中数学 来源: 题型:
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() ≌
≌![]() .
.
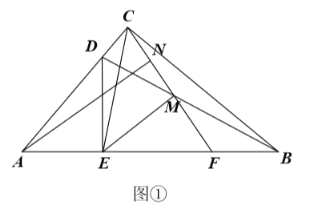
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
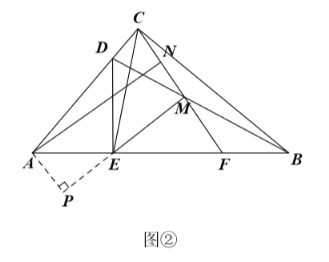
(3)如图②,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
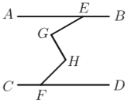
【题目】如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,点A、B、C均在格点上,按下述要求画图并标注相关字母.

(1)画线段AB,画射线BC,画直线AC;
(2)过点B画线段BD⊥AC,垂足为点D;
(3)取线段AB的中点E,过点E画BD的平行线,交AC于点F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题.
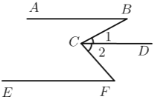
(1)探究:如图,![]() ,试说明
,试说明![]() .
.
(2)拓展:如图,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,利用探究结论求
,利用探究结论求![]() 的度数.
的度数.
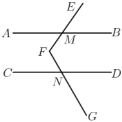
(3)应用:如图,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在
在![]() 与
与![]() 之间,
之间,![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为______度.
的大小为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题:
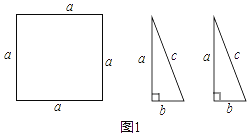
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
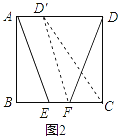
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
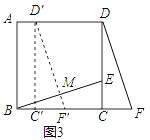
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形;
(2)若AC=8,EF=6,求BF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com