
����Ŀ�����ⱳ������ѧ�������ʦ��ʾ���⣬��ͼ1���б߳�Ϊa��������ֽƬһ�ţ����߳��ֱ�Ϊa��b��c��ȫ��ֱ��������ֽƬ���ţ���![]() ��������������ֽƬƴ��һ��ͼ�����������ͼ����ij���ֽ�����ת��ƽ�Ʊ任֮�����һ�����⣨������������������������Ը���a��b��ֵ�ȵȣ���
��������������ֽƬƴ��һ��ͼ�����������ͼ����ij���ֽ�����ת��ƽ�Ʊ任֮�����һ�����⣨������������������������Ը���a��b��ֵ�ȵȣ���
������⣺
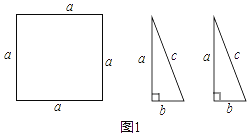
����������ѧϰС��ƴ��ͼ������������⣬������������������⣮
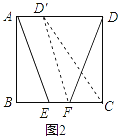
��1����������С������������ǣ���ͼ2������DFC�Ƶ�F��ʱ����ת��ʹ��Dǡ������AD���ϵĵ�D�����������ʱ�ı���AEFD����ʲô�����ı��Σ�������֤����
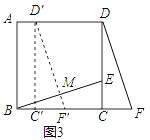
��2����ϣ����С������������ǣ���ͼ3����MΪBE�е㣬����DCF����ƽ����DFǡ�ù���Mʱֹͣ���Ҳ�������a=6��b=2�����DCFƽ�Ƶľ��룮
�������£�
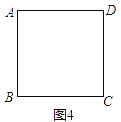
��3�������������С���ͬѧ��������ͼ4�Ŀհ״���ʵ������ƴ����ͼ�������������任ͼ�����ں��ߴ�д������������⣮�����ؽ��
����������⣺________��
���𰸡�![]() .
.
��������
ģ�£�1���ͣ�2���������a=6��b=2ʱ����M��N�ֱ�ΪAD��BC�е㣬����MNF��CB�����ƶ���ʹ��M���ڵ�A��ʱ����AB�ϣ�AF����ME��G������GEF�������
��1��֤������FG��AD��
���ı���ABCD�������Σ�
���ADC=��C=90����AD��BC��
���ı���GFCD�Ǿ��Σ�
��GD=FC=b��
��FD=FD�䣬
��D��G=DG=b��
��AD��=AD��2DG=a��2b��
��BE=FC=b��
��EF=BC��2FC=a��2b��
��AD��=EF��
��AD����EF��
���ı���AEFD����ƽ���ı���
��2���⣺��ƽ��֪����C��D��F��=��CDF=��EBC��
�ߡ�C��D��F��+��BF��M=90����
���MBF��+��BF��M=90����
���BMF��=90����
�ɹ��ɶ����ã�BE=![]() =2
=2![]() ��
��
�ߵ�MΪBE�е㣬
��BM=![]() ��
��
�ߡ�BMF��=��BCE����MBF��=��CBE��
���BMF���ס�BCE��
�� ![]() ��
��
��![]() ��
��
��BF��=![]() ��
��
��BF=BC+CF=8��
��F��F=BF��BF��=![]() ��
��
���DCFƽ�Ƶþ���Ϊ![]() ��
��
��3�������������
��a=6��b=2ʱ����M��N�ֱ�ΪAD��BC�е㣬����MNF��CB�����ƶ���ʹ��M���ڵ�A��ʱ����AB�ϣ�AF����ME��G�����GEF�������
��ͼ��
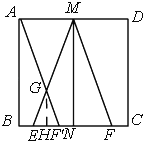
��MN=BC=b=6��NF=BF��=a=2��
��FC=BE=F��N=1��
��EF��=1��
��EH=F��H=![]() EF��=
EF��=![]() ��
��
��GH��AB��
��![]()
��![]() ��
��
��GH=![]() ��
��
��S��GEF��=![]() ��EF���GH=
��EF���GH=![]() .
.


 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ֪��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() .
.
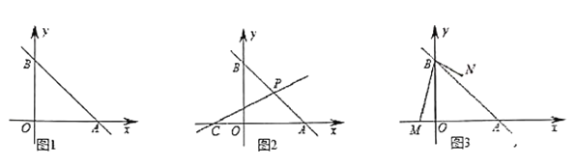
��1��ֱ��д��![]() ��ֵΪ______.
��ֵΪ______.
��2����ͼ2��![]() Ϊ
Ϊ![]() �Ḻ������һ�㣬��
�Ḻ������һ�㣬��![]() ���ֱ��
���ֱ��![]() ��
��![]() ����
����![]() ���е�
���е�![]() ����
����![]() Ϊ
Ϊ![]() ����һ���㣬��
����һ���㣬��![]() ��
��![]() ��ֱ�ֱ��
��ֱ�ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ.
��ֵ.
��3����ͼ3����֪��![]() ����
����![]() Ϊֱ��
Ϊֱ��![]() �Ҳ�һ�㣬������
�Ҳ�һ�㣬������![]() �����
�����![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
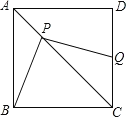
����Ŀ����ͼ,������ABCD,��P�ǶԽ���AC��һ��,����BP,��P��PQ��BP,PQ��CD��Q,��AP=![]() ��CQ=3�����ı���PBCQ�����Ϊ_______.
��CQ=3�����ı���PBCQ�����Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ�����ͼ2����ͼ1�������£���DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ�ڵ�M��N.�Խ���������⣺

(1)��ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ��
(2)��ϸ�۲죬��ͼ2�С�8���Ρ��ж��ٸ���
(3)ͼ2�У�����D��50�㣬��B��40��ʱ�����P�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������Ǵ�������������ij����������Ϊ���������ʵЧ�����������˲��־���С��һ��ʱ�������������ķ������������ͼ���������������������������в�������ͳ��ͼ��
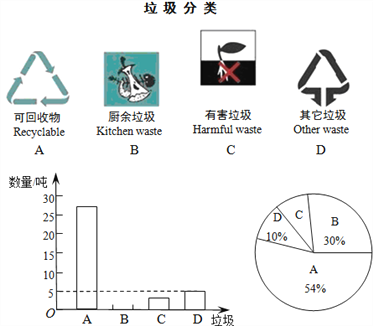
����ͼ������������⣺
��1���뽫����ͳ��ͼ����������
��2��������ͳ��ͼ�У������D����������Ӧ��Բ�Ľǵ��������������ȣ�
��3���ڳ��������У��������к����������������������֣�
��4�����鷢�֣��ڿɻ������з�ֽ����Լռ![]() ����ÿ����1�ַ�ֽ������ֽ0.85�֣�����ó���ÿ�²�������������Ϊ10000�֣���ȫ�����ദ������ôÿ�»��յķ�ֽ������ֽ���ٶ֣�
����ÿ����1�ַ�ֽ������ֽ0.85�֣�����ó���ÿ�²�������������Ϊ10000�֣���ȫ�����ദ������ôÿ�»��յķ�ֽ������ֽ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽������ͼ������![]() ��
��![]() �Ϸ�������
�Ϸ�������![]() ��
��![]() �·���
�·���![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�
�������֣���1����![]() ��
��![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
��2������̽������![]() �̶����䣬��
�̶����䣬��![]() ����Ϊ
����Ϊ![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
̽�����֣���3������ɣ�1����2��ʱ��С������![]() ��
��![]() ֮�����һ���̶���������ϵ������ΪС��˵�Ķ�����˵�����ɣ�
֮�����һ���̶���������ϵ������ΪС��˵�Ķ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��ͨ�������ĵ�����Ƴ���ij�ֶ���20��ĸ���Ϊ0.8���25��ĸ�����0.5���30��ĸ�����0.3������20������ֶ���25��ĸ���Ϊ���٣�����25������ֶ���30��ĸ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
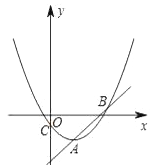
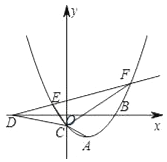
����Ŀ����ͼ��������![]() ��m��0���Ķ���ΪA����y���ڵ�C��
��m��0���Ķ���ΪA����y���ڵ�C��
��1�������A�����꣨�ú�m��ʽ�ӱ�ʾ����
��2��ƽ��ֱ��y=x������A��������C����һ��B��ֱ��AB�·�������C��һ��P�����P��ֱ��AB��������
��3����ֱ��AC��x���ڵ�D��ֱ��AC����x��ԳƵ�ֱ�߽�������C��E��F���㣮����ECF=90������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
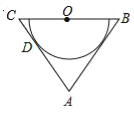
����Ŀ����ͼ������ABC�У�AB=AC��OΪBC���е㣬AC���ԲO�����ڵ�D��
��1����֤��AB�ǰ�ԲO����Բ�����ߣ�
��2����cos��ABC=![]() ��AB=12�����ԲO����Բ�İ뾶��
��AB=12�����ԲO����Բ�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com