
【题目】如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
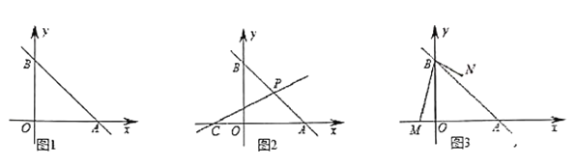
(1)直接写出![]() 的值为______.
的值为______.
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
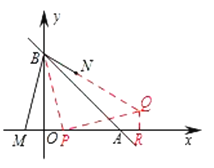
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
【答案】(1)k=-1;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)将![]() 代入
代入![]() ,求解即可得出;
,求解即可得出;
(2)先求得直线![]() 为
为![]() ,用含t的式子表示MN,根据
,用含t的式子表示MN,根据![]() 列出方程
列出方程![]() ,分三种情况讨论,可得到
,分三种情况讨论,可得到![]() 或
或![]() ;
;
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,再证出
,再证出![]() ,得到直线
,得到直线![]() 的解析式为
的解析式为![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,可得出
,可得出![]() .
.
解:(1)将![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() .
.
故答案为:![]()
(2)∵在直线![]() 中,令
中,令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴直线![]() 为
为![]() ,
,
∵![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,分情况讨论:
,分情况讨论:
①当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
②当![]() 时,
时,![]() ,解得:
,解得:![]() .
.
③当![]() 时,
时,![]() ,解得:
,解得:![]() ,舍去.
,舍去.
综上所述:![]() 或
或![]() .
.
(3)在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,作
,作![]() 交直线
交直线![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是射线
是射线![]() 上一点,
上一点,![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
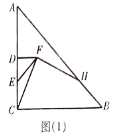
(1)如图(1),当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并加以证明;
的数量关系,并加以证明;
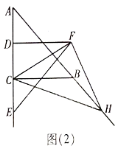
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当
的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当![]() 和
和![]() 面积相等时,点
面积相等时,点![]() 与点
与点![]() 之间的距离;如果不成立,请说明理由.
之间的距离;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
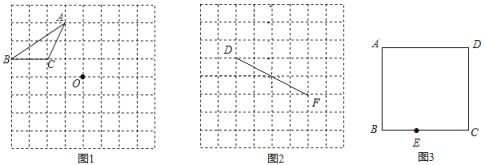
【题目】(1)如图1,方格纸中的每个小方格都是边长为1个单位的正方形,![]() 的顶点以及点
的顶点以及点![]() 均在格点上.
均在格点上.
①直接写出![]() 的长为______;
的长为______;
②画出以![]() 为边,
为边,![]() 为对角线交点的平行四边形
为对角线交点的平行四边形![]() .
.
(2)如图2,画出一个以![]() 为对角线,面积为6的矩形
为对角线,面积为6的矩形![]() ,且
,且![]() 和
和![]() 均在格点上(
均在格点上(![]() 、
、![]() 、
、![]() 、
、![]() 按顺时针方向排列).
按顺时针方向排列).
(3)如图3,正方形![]() 中,
中,![]() 为
为![]() 上一点,在线段
上一点,在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() .(要求用无刻度的直尺画图,不准用圆规,不写作法,保留画图痕迹)
.(要求用无刻度的直尺画图,不准用圆规,不写作法,保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
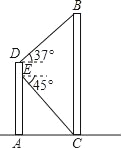
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
查看答案和解析>>
科目:初中数学 来源: 题型:
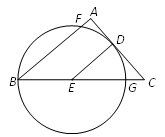
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
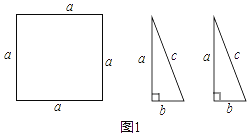
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题:
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
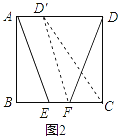
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
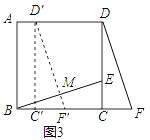
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
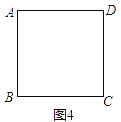
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题:________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com