
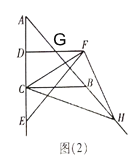
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是射线
是射线![]() 上一点,
上一点,![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
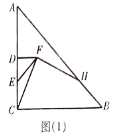
(1)如图(1),当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并加以证明;
的数量关系,并加以证明;
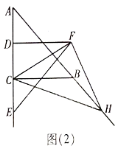
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当
的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当![]() 和
和![]() 面积相等时,点
面积相等时,点![]() 与点
与点![]() 之间的距离;如果不成立,请说明理由.
之间的距离;如果不成立,请说明理由.
【答案】(1)![]() ,证明见解析;(2)依然成立,点
,证明见解析;(2)依然成立,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() .理由见解析.
.理由见解析.
【解析】
(1)做辅助线,通过已知条件证得![]() 与
与![]() 是等腰直角三角形.证出
是等腰直角三角形.证出![]() ,利用全等的性质即可得到
,利用全等的性质即可得到![]() .
.
(2)设AH,DF交于点G,可根据ASA证明△FCE≌△HFG,从而得到![]() ,当
,当![]() 和
和![]() 均为等腰直角三角形当他们面积相等时,
均为等腰直角三角形当他们面积相等时,![]() .利用勾股定理可以求DE、CE的长,即可求出CE的长,即可求得点
.利用勾股定理可以求DE、CE的长,即可求出CE的长,即可求得点![]() 与点
与点![]() 之间的距离.
之间的距离.
(1)![]()
证明:延长![]() 交
交![]() 于点
于点![]()
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]()
∵![]() 于点
于点![]() ,且
,且![]() ,
,
∴![]() ,
,![]() 与
与![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]()
∴![]()
∵![]() 于点
于点![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
∴![]()
∴![]() ;
;
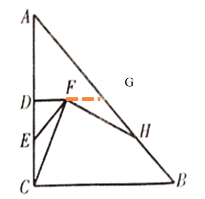
(2)依然成立
理由:设AH,DF交于点G,
由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG=![]() BC,DC=
BC,DC=![]() AC,
AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中
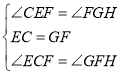 ,
,
∴△FCE≌△HFG(ASA),
∴HF=FC.
由(1)可知![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
当他们面积相等时,![]() .
.
∴![]()
∴![]()
∴点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
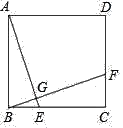
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
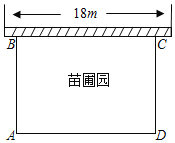
【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF过点A,且ME=30步,NF=750步,则正方形的边长为( )
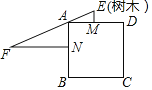
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省衢州市)已知二次函数![]() 的图象,如图所示
的图象,如图所示
(1)根据方程的根与函数图象之间的关系,将方程![]() 的根在图上近似地表示出来(描点),并观察图象,写出方程
的根在图上近似地表示出来(描点),并观察图象,写出方程![]() 的根(精确到0.1).
的根(精确到0.1).
(2)在同一直角坐标系中画出一次函数![]() 的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
(3)如图,点P是坐标平面上的一点,并在网格的格点上,请选择一种适当的平移方法,使平移后二次函数图象的顶点落在P点上,写出平移后二次函数图象的函数表达式,并判断点P是否在函数![]() 的图象上,请说明理由.
的图象上,请说明理由.
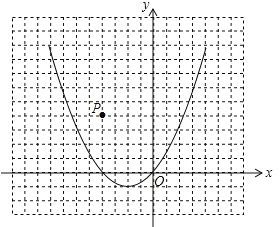
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,C=90°,O在AC上,以OC为半径作⊙O,切AB于D点,且BC=BD.
(1)求证:AB为⊙O的切线;
(2)若BC=6,sinA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,P点在⊙O上为一动点,求BP的最大值与最小值.
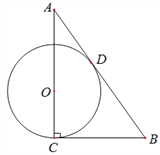
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
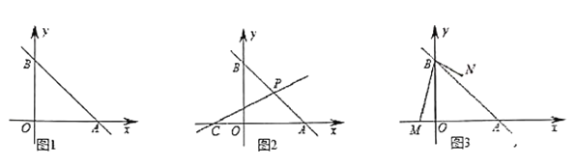
(1)直接写出![]() 的值为______.
的值为______.
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com