
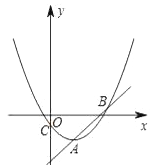
【题目】如图,抛物线![]() (m<0)的顶点为A,交y轴于点C.
(m<0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)平移直线y=x经过点A交抛物线C于另一点B,直线AB下方抛物线C上一点P,求点P到直线AB的最大距离
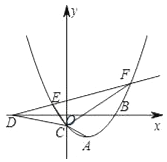
(3)设直线AC交x轴于点D,直线AC关于x轴对称的直线交抛物线C于E、F两点.若∠ECF=90°,求m的值.
【答案】(1)顶点A坐标![]() ;(2)P到直线AB的距离d的最大值为
;(2)P到直线AB的距离d的最大值为 ![]() ;(3)m=1
;(3)m=1![]() .
.
【解析】(1)利用配方法即可解决问题;
(2)过点P作PQ∥y轴交AB于Q,如图1中,设P![]() ,首先求出PQ的最大值,点P到直线AB的最大距离d=
,首先求出PQ的最大值,点P到直线AB的最大距离d=![]() ,由此即可即可解决问题;
,由此即可即可解决问题;
(3)过点C作MN∥x轴,过点E作EM⊥MN于M,过点F作FN⊥MN于N,如图2中,设E(x1,y1)、F(x2,y2),由Rt△EMC∽Rt△CNF,得![]() ,即
,即 ![]() ,化简得:y1y2-m(y1+y2)+m2=-x1x2,再由
,化简得:y1y2-m(y1+y2)+m2=-x1x2,再由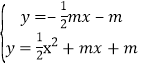 ,消去y,整理得:x2+3mx+4m=0,利用根与系数关系,转化为关于m的方程即可解决问题.
,消去y,整理得:x2+3mx+4m=0,利用根与系数关系,转化为关于m的方程即可解决问题.
(1)∵![]() ,
,
∴顶点A坐标![]() ;
;
(2)∵直线AB的解析式为![]() ,
,
设P ![]() ,
,
过点P作PQ∥y轴交AB于Q,如图1中,
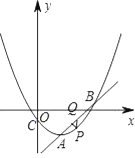
∴Q![]() ,
,
∴PQ=![]()
=![]()
=![]() ,
,
当a=1-m 时,PQ有最大值为![]() ,
,
∵PQ与直线AB的夹角为45°,
∴P到直线AB的距离d的最大值为 ![]() ;
;
(3)A(﹣m,﹣![]() m2+m)、C(0,m),
m2+m)、C(0,m),
A′(﹣m,![]() m2﹣m,)、C′(0,﹣m),
m2﹣m,)、C′(0,﹣m),
∴直线EF的解析式为y=﹣![]() mx﹣m,
mx﹣m,
设E(x1 , y1)、F(x2 , y2),
过点C作MN∥x轴,过点E作EM⊥MN于M,过点F作FN⊥MN于N,
∵∠ECF=90°,
∴∠ECM+∠FCN=90°,∠FCN+∠CFN=90°,
∴∠ECM=∠CFN,∵∠EMC=∠FNC=90°,
∴Rt△EMC∽Rt△CNF,∴![]() ,
,
即 ![]() ,
,
化简得:y1y2﹣m(y1+y2)+m2=﹣x1x2,
由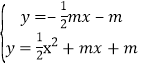 ,消去y,整理得:x2+3mx+4m=0,
,消去y,整理得:x2+3mx+4m=0,
∴x1+x2=﹣3m,x1x2=4m,
y1y2=(﹣![]() mx1﹣m)(﹣
mx1﹣m)(﹣![]() mx2﹣m)=﹣
mx2﹣m)=﹣![]() m3+m2,
m3+m2,
y1+y2=![]() m2﹣2m,
m2﹣2m,
∴﹣![]() m3+m2﹣m(
m3+m2﹣m(![]() m2﹣2m)+m2=﹣4m,
m2﹣2m)+m2=﹣4m,
∴m(m-2m-2)=0
解得m=1![]() 或1+
或1+![]() 或0,
或0,
∵m<0,∴m=1![]() .
.


科目:初中数学 来源: 题型:
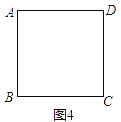
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题:
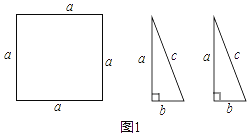
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
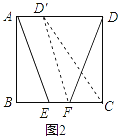
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
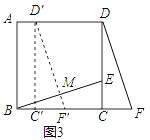
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
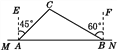
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干大小相同的小立方体块搭一个几何体,使得从正面和上面看到这个几何体的形状图如图所示,其中从上面看到的形状图的小正方形中的字母表示该位置小立方体的个数.请解答:

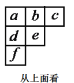
(1)![]() 表示几?
表示几?![]() 的最大值是多少?
的最大值是多少?
(2)这个几何体最少是用多少个小立方体搭成的?最多呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形;
(2)若AC=8,EF=6,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com