
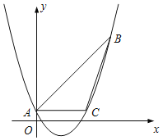
【题目】如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
(1)求这条抛物线的解析式.
(2)求tan∠ABC的值.
(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(4,1)或E(﹣3,1).
;(3)E(4,1)或E(﹣3,1).
【解析】
(1)将点A和点B的坐标代入抛物线的解析式求得a、c的值即可;
(2)过点B作BH⊥AC交AC延长线于点H,过点C作CG⊥AB于点G,先证明△ABH和△ACG均为等腰直角三角形,再求出CG和BG的长,然后依据锐角三角函数的定义求解即可;
(3)过点D作DK⊥AC,垂足为K,先证明△DCK为等腰直角三角形,则∠DCK=∠BAC,当![]() 或
或![]() 时,△CDE与△ABC相似,然后可求得CE的长.
时,△CDE与△ABC相似,然后可求得CE的长.
解:(1)∵抛物线y=ax2﹣2x+c经过点A(0,1)和点B(9,10),
∴![]() ,解得
,解得![]() .
.
∴这条抛物线的解析式为![]() .
.
(2)过点B作BH⊥AC交AC延长线于点H,
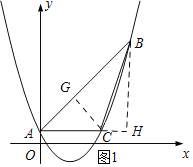
∵AC∥x轴,A(0,1),B(9,10),∴H(9,1),∴BH=AH=9.
又∵∠BHA=90°,∴△HAB是等腰直角三角形,∴∠HAB=45°.
∵AC∥x轴,A(0,1),对称轴为直线![]() ,∴C(6,1).
,∴C(6,1).
过点C作CG⊥AB,垂足为点G,
∵∠GAC=45°,∠AGC=90°,∴![]() ,∴
,∴![]() .
.
又∵在Rt△ABH中,![]() ,∴
,∴![]() .
.
∴在Rt△BCG中,![]() .
.
(3)如图2所示:过点D作DK⊥AC,垂足为K,

∵点D是抛物线![]() 的顶点,∴D(3,﹣2).
的顶点,∴D(3,﹣2).
∴K(3,1),∴CK=DK=3.
又∵∠CKD=90°,∴△CDK是等腰直角三角形,∴∠DCK=45°
又∵∠BAC=45°,
∴∠DCK=∠BAC.
∴要使△CDE与△ABC相似,则点E在点C的左侧.
当![]() 时,则
时,则![]() ,∴EC=2,∴E(4,1);
,∴EC=2,∴E(4,1);
当![]() 时,则
时,则![]() ,∴EC=9,∴E(﹣3,1).
,∴EC=9,∴E(﹣3,1).
综上所述,当△CDE与△ABC相似时,点E的坐标为(4,1)或(﹣3,1).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.求甲、乙两种图书每本价格分别为多少元?我们设乙图书每本价格为x元,则可得方程( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. 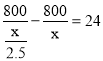
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC是⊙O的一条弦,D为弧BC的中点,作DE⊥AC,垂足为AC的延长线上的点E,连接DA,DB.
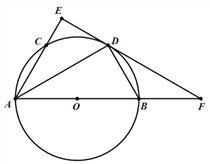
(1)求证:DE为⊙O的切线;
(2)试探究线段AB,BD,CE之间的数量关系,并说明理由;
(3)延长ED交AB的延长线于F,若AD=DF,DE=![]() ,求⊙O的半径;
,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,点K为弧AC上的一个动点(K不与A,C重合),AK,DC延长线交于点F,连接CK.
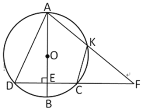
(1)求证:△ADF∽△CKF
(2)若AB=10,CD=6,求tan∠CKF的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,顶点为A的抛物线与x轴交于B、C两点,与y轴交于点D,已知A(1,4),B(3,0).
(1)求抛物线对应的二次函数表达式;
(2)探究:如图1,连接OA,作DE∥OA交BA的延长线于点E,连接OE交AD于点F,M是BE的中点,则OM是否将四边形OBAD分成面积相等的两部分?请说明理由;
(3)应用:如图2,P(m,n)是抛物线在第四象限的图象上的点,且m+n=﹣1,连接PA、PC,在线段PC上确定一点M,使AN平分四边形ADCP的面积,求点N的坐标.提示:若点A、B的坐标分别为(x1,y1)、(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
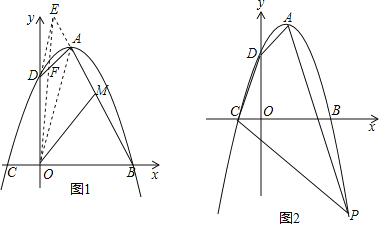
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的两个动点(与点
上的两个动点(与点![]() 、
、![]() 、
、![]() 不重合),且始终保持
不重合),且始终保持![]() ,
,![]() ,
,![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
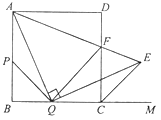
(1)求证:![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,并求出此时
,并求出此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(新知探究)新定义:平面内两定点 A, B ,所有满足![]() k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
(问题解决)如图,在ABC 中,CB 4 , AB 2AC ,则ABC 面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市九年级学生身体素质情况,从全市九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
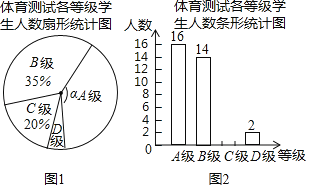
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 °,把图2条形统计图补充完整;
(3)全市九年级有学生6200名,如果全部参加这次体育科目测试,请估计不及格的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点
,点![]() 在
在![]() 轴上,以
轴上,以![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 轴上,且在点
轴上,且在点![]() 上方,过点
上方,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点,如果点
为切点,如果点![]() 在第一象限,则称
在第一象限,则称![]() 为点
为点![]() 的离点.例如,图1中的
的离点.例如,图1中的![]() 为点
为点![]() 的一个离点.
的一个离点.
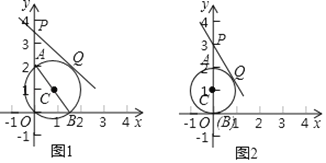
(1)已知点![]() ,
,![]() 为
为![]() 的离点.
的离点.
①如图2,若![]() ,则圆心
,则圆心![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________;
的长为__________;
②若![]() ,求线段
,求线段![]() 的长;
的长;
(2)已知![]() ,直线
,直线![]() .
.
①当![]() 时,若直线
时,若直线![]() 上存在
上存在![]() 的离点
的离点![]() ,则点
,则点![]() 纵坐标
纵坐标![]() 的最大值为__________;
的最大值为__________;
②记直线![]() 在
在![]() 的部分为图形
的部分为图形![]() ,如果图形
,如果图形![]() 上存在
上存在![]() 的离点,直接写出
的离点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com