
科目:初中数学 来源: 题型:解答题
 如图,已知BD,CE分别为∠ABC,∠ACB的平分线,AM⊥CE于M,AN⊥BD于N.求证:MN=$\frac{1}{2}$(AB+AC-BC).
如图,已知BD,CE分别为∠ABC,∠ACB的平分线,AM⊥CE于M,AN⊥BD于N.求证:MN=$\frac{1}{2}$(AB+AC-BC).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )
如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
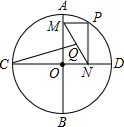 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.
如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.
如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16cm | B. | 12cm | C. | 24cm | D. | 36cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com