
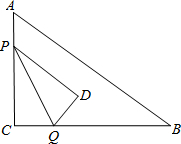
 在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由.
在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由. 分析 可通过构建相似三角形来求解.延长PD交BC于M,通过相似三角形QMD和三角形ABC得出的关于OD,QM,AC,AB的比例关系式,可得出QM的表达式,然后根据PD∥AB得出的关于CP,CA,CM,CB的比例关系式求出t的值
解答 解:设存在时刻t,使得PD∥AB,延长PD交BC于点M,如图,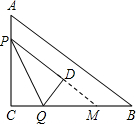
若PD∥AB,则∠QMD=∠B,
又∵∠QDM=∠C=90°,
∴Rt△QMD∽Rt△ABC,
从而$\frac{QM}{AB}$=$\frac{QD}{AC}$,
∵QD=CQ=4t,AC=12,
AB=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴QM=$\frac{20}{3}$.
若PD∥AB,则$\frac{CP}{CA}$=$\frac{CM}{CB}$,
得$\frac{12-3t}{12}$=$\frac{4t+\frac{20}{3}t}{16}$,
解得t=$\frac{12}{11}$.
∴当t=$\frac{12}{11}$秒时,PD∥AB.
点评 本题考查了相似三角形的判定与性质,以及勾股定理的应用,本题是一道动态几何题,综合性较强,计算量比较大,其中确定出PD∥AB时t的值是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
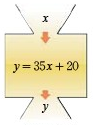 地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.
地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
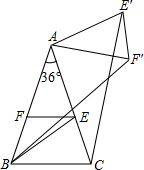 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
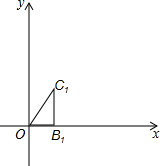 如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com