
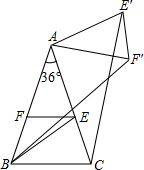
 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB. 分析 把△AEF绕点A逆时针旋转AE′与过点C与AB平行的直线相交于M、N,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
解答 解:在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,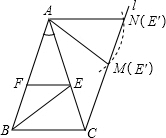
①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,
所以,∠BAM=∠ABC=72°,
又∵∠BAC=36°,
∴α=∠CAM=36°;
②当点E的像E′与点N重合时,
∵CE′∥AB,
∴∠AMN=∠BAM=72°,
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180°-72°×2=36°,
∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,
综上所述,当旋转角为36°或72°时,CE′∥AB.
故答案为:36°或72°.
点评 此题主要考查了旋转的性质以及等腰三角形的性质和等腰梯形的性质等知识,根据数形结合熟练掌握相关定理是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
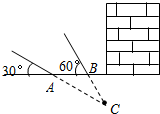 北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).
北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
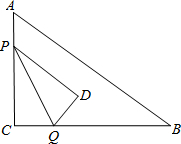 在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由.
在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
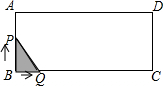 矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )
矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )| A. | 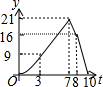 | B. | 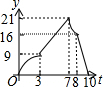 | C. | 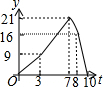 | D. | 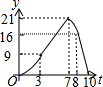 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
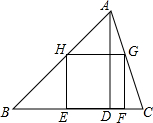 如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,
如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 冰箱 | 彩电 | |
| 售价(元/台) | 2500 | 2000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com