
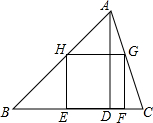
 如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,
如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,分析 (1)根据四边形EFGH是△ABC内接正方形,得出HG∥BC,得出△AHG与△ABC相似即可;
(2)根据题意易证△AHG∽△ABC,列出比例关系,可以解出内接正方形EFGH的边长.
解答 解:(1)相似,理由如下:
∵四边形EFGH是△ABC内接正方形,
∴HG∥BC,
∴△AHG∽△ABC;
(2)设AD与HG的交点为M,
∵△AHG∽△ABC,
∴$\frac{HG}{BC}=\frac{AM}{AD}$,
$\frac{HG}{21}=\frac{15-HG}{15}$,
解得:$HG=\frac{35}{4}$,
故内接正方形EFGH的边长为$\frac{35}{4}$.
点评 本题主要考查正方形的性质,三角形相似等知识点,不是很难.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
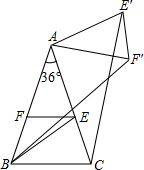 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
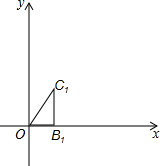 如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
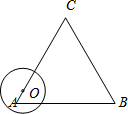 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com