
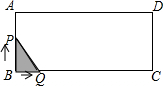
 矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )
矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )| A. | 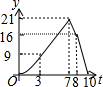 | B. | 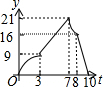 | C. | 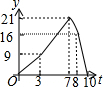 | D. | 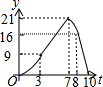 |
分析 分四种情况:①当0<t≤3时,△PBQ是Rt△,根据三角形的面积公式可得y=t2;②当3<t≤7时,三角形高不变,根据三角形的面积公式可得y=3t;③当7<t≤8时,根据三角形的面积公式可得y=$\frac{1}{2}$t(2t-14)=t2-7t;④当8<t≤10时,三角形底不变,根据三角形的面积公式可得y=$\frac{1}{2}$×8(20-2t)=80-8t;根据函数关系即可得到y与t的函数大致图象.
解答 解:①当0<t≤3时,△PBQ是Rt△,y=$\frac{1}{2}$×t×2t=t2;
②当3<t≤7时,y=$\frac{1}{2}$×t×6=3t;
③当7<t≤8时,y=$\frac{1}{2}$t(2t-14)=t2-7t;
④当8<t≤10时,y=$\frac{1}{2}$×8(20-2t)=80-8t;
观察各选项可知,y与t的函数图象大致是选项D.
故选:D.
点评 考查了动点问题的函数图象和三角形的面积,关键是得到y与t的函数,注意要进行分类讨论.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
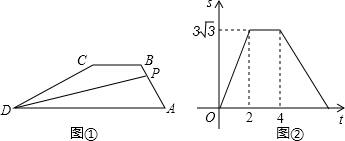
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
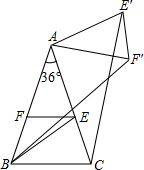 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
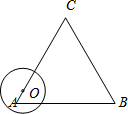 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{240}$天 | B. | $\frac{m}{250}$天 | C. | $\frac{m}{260}$天 | D. | $\frac{m}{270}$天 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com